Bionic Turtle Super Admin
Administrator
Note: this is inspired by @Jayanthi Sankarans' observation at https://forum.bionicturtle.com/thre...tal-asset-pricing-models-video-tutorial.8166/
Let's assume:
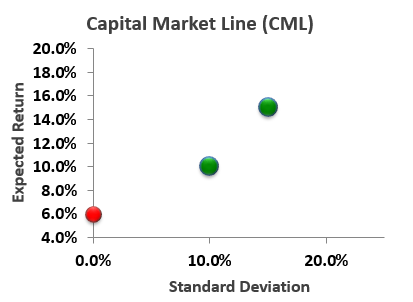
Let's assume:
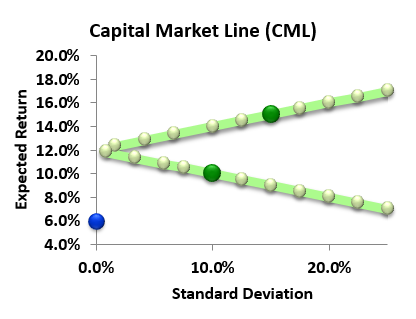
- Risk-free asset rate is 6.0% (red dot)
- Asset A has expected return and standard deviation of 10% (green dot)
- Asset B has expected return and standard deviation of 15% (second green dot)
- Their correlation = -1.0; i.e., perfect negative correlation


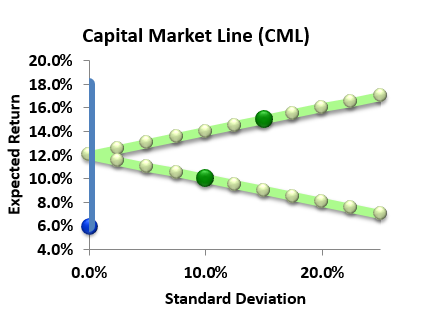
 I've assumed (taught, been taught) that the CML is the line which mixes two components: the market portfolio (i.e., the mix of risky-only assets with the highest Sharpe ratio) and the risk-free asset. Therefore, my initial answer (to myself) was exactly what
I've assumed (taught, been taught) that the CML is the line which mixes two components: the market portfolio (i.e., the mix of risky-only assets with the highest Sharpe ratio) and the risk-free asset. Therefore, my initial answer (to myself) was exactly what