New practice questions
- P2.T9.705. The electronification of fixed income markets https://forum.bionicturtle.com/thre...ctronification-of-fixed-income-markets.10322/
- P2.T9.706. Negative policy rates https://forum.bionicturtle.com/threads/p2-t9-706-negative-policy-rates.10331/
- P2.T9.707. Corporate debt in emerging economies https://forum.bionicturtle.com/threads/p2-t9-707-corporate-debt-in-emerging-economies.10339/
- Practice exam scores (FRM Part 2) https://forum.bionicturtle.com/threads/practice-exam-scores-and-actual-exam-result-pt-2.10307/
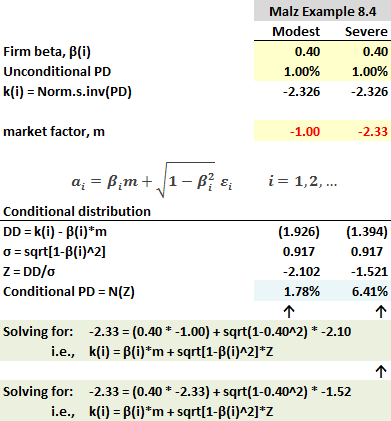
- My explanation of Malz’ single-factor credit risk model, thank you for asking @RobKing https://forum.bionicturtle.com/threads/p2-t6-304-single-factor-credit-risk-model.6806/#post-48931
- Good point by @bpdulog on the imprecise definition of illiquidity as a potential red flag (Mirabile probably does not mean to say that “a high percentage of illiquid investments” is a red flag; rather, he probably should say “onerous liquidity terms for investors”) https://forum.bionicturtle.com/threads/p2-t8-414-hedge-fund-due-diligence-continued.8066/#post-48934
- Does current (credit) exposure include credit exposure over the remaining life of the swap? https://forum.bionicturtle.com/threads/l1-t3-176-currency-swap-valuation.4587/page-4#post-48933
- Clarification of margin requirements when writing naked stock options https://forum.bionicturtle.com/thre...exchange-traded-options-hull.9357/#post-48918
- Thank you @farahm for wordsmith improvements https://forum.bionicturtle.com/threads/p2-t9-706-negative-policy-rates.10330/#post-48922
- I agree with @bpdulog that Stulz is inaccurate here in regard to the total return swap (TRS) https://forum.bionicturtle.com/threads/stulz-ch-18-total-return-swap.10319/
- What is par yield? https://forum.bionicturtle.com/threads/l1-t3-158-bond-price-using-spot-rates.4481/page-2#post-48903
- Another good point by @bpdulog: Why does Litterman call it the “Risk Management Unit (RMU)” if, you know, it does not manage risk? https://forum.bionicturtle.com/thre...n-on-performance-measurement.8022/#post-48901
- How to reconcile continuous and discrete forward rates https://forum.bionicturtle.com/thre...m-spot-rates-hull-vs-tuckman.5406/#post-48897
- If the commodity producer’s future sales price is predetermined, then a long hedge is warranted; if the futures sales price is not predetermined (i.e., the typical use case), then a short hedge is warranted https://forum.bionicturtle.com/threads/predetermined-future-price.9283/#post-48891
- The test of alpha (which determines the number of years required for significant alpha) is just a significance test https://forum.bionicturtle.com/thre...-of-performance-topic-review.7744/#post-48895
- Nuance in Jorion’s surplus at risk (SaR) calculation https://forum.bionicturtle.com/threads/p2-t8-12-surplus-at-risk-sar.5488/page-2#post-48851
- Is Bitcoin vulnerable to a fake identity attack? https://forum.bionicturtle.com/thre...tcoin-and-what-are-bitcoins.10280/#post-48849
- Hull’s Question 2.15 (how to estimate the additional equity required to maintain solvency with 99.9% confidence) https://forum.bionicturtle.com/thre...ctions-and-definitions-hull.10242/#post-48804
- What exactly does Andrew Ang mean when he says there are not significant illiquidity risk premiums ACROSS asset classes, but there are large illiquidity risk premiums WITHIN asset classes? https://forum.bionicturtle.com/thre...nclusion-of-illiquid-assets.10269/#post-48828
- It’s helpful to remember that every univariate OLS regression line must pass through the average value of both the independent and dependent variables https://forum.bionicturtle.com/thre...ctive-benchmarks-andrew-ang.10204/#post-48826
- Good observation (again) by @bpdulog that Ang’s alphas for Buffet’s Berkshire Hathaway aren’t highly significant, they are more like barely significant https://forum.bionicturtle.com/thre...ay-versus-its-benchmark-ang.10236/#post-48827
- Money Market Funds and the New SEC Regulation http://libertystreeteconomics.newyo...-market-funds-and-the-new-sec-regulation.html
- After Exiting Capital Controls, Iceland Still Wary of Private Investors https://www.nytimes.com/2017/03/21/...-iceland-still-wary-of-private-investors.html
- Why cybersecurity is now top of the agenda for the world’s decision-makers https://medium.com/world-economic-f...orlds-decision-makers-fb74e17b09b5#.vtu7e2rsc
- Fintech—A Brave New World for the Financial Sector? By Christine Lagarde https://blog-imfdirect.imf.org/2017/03/21/fintech-a-brave-new-world-for-the-financial-sector/
- The First Climate Model Turns 50, And Predicted Global Warming Almost Perfectly https://medium.com/starts-with-a-ba...ming-almost-perfectly-3c0854932a4a#.u97340m8w
- The Extreme Temperature Index: Identifying Which Records are Most Significant https://www.wunderground.com/blog/J...index-identifying-which-records-are-most-sign
- Banks and Tech Firms Battle Over Something Akin to Gold: Your Data https://www.nytimes.com/2017/03/23/...le-over-something-akin-to-gold-your-data.html
- Quandl and Forecasting https://www.rstudio.com/rviews/2017/03/17/quandl-and-forecasting/
- Should College Students Be Required to Take a Course in Personal Finance? https://www.wsj.com/articles/should...-take-a-course-in-personal-finance-1489975500 "Being knowledgable about money management, budgeting and finance is no guarantee of success in life. But ignorance about such concepts often comes at great cost."
- Two in Five Americans Say They’ll Need $1 Million to Retire (A new survey finds our expectations at odds with the financial reality of today’s retirees) https://www.bloomberg.com/news/arti...mericans-say-they-ll-need-1-million-to-retire
- When Others Die, Tontine Investors Win Retiring https://www.nytimes.com/2017/03/24/business/retirement/tontines-retirement-annuity.html
- Credit Card Fraud in the US: Exceptionally High Risk, and a Plan for Mitigating It http://www.garp.org/#!/risk-intelligence/all/all/a1Z40000003PQU5EAO
- The Journey of Humankind: How Money Made Us Modern http://news.nationalgeographic.com/2017/03/money-human-origins-journey-humankind/
- The Return of Economic History http://www.booksandideas.net/The-Return-of-Economic-History.html
- How to short Uber (and other private companies) https://medium.com/@avishbhama/how-to-short-uber-and-other-private-companies-7754b8fb7de1#.5kwspuxmv
- 2017 Corporate Human Rights Benchmark https://www.corporatebenchmark.org/
- Increasing Risk Complexity Outpaces ERM Oversight http://www.riskmanagementmonitor.com/increasing-risk-complexity-outpaces-erm-oversight/
- Beyond Category: ESG Factors Turn Mainstream https://annual.cfainstitute.org/2017/03/21/beyond-category-esg-factors-turn-mainstream/
- Capital Group takes on the passive investors https://www.ft.com/content/5e1df770-0d58-11e7-a88c-50ba212dce4d “But Capital’s analysis of historic fund performance — research that has been corroborated by Morningstar, an industry data provider — has shown that two factors are strong indicators of long-term, market-beating returns: fund managers having plenty of their own money in a fund; and low fees … Capital won permission from regulators this year to start selling what it calls “clean shares”, which, unlike most mutual fund share classes, do not include a distribution fee baked in. Clean shares will include only Capital’s own management fee.”
- A Rogue Trader Blames the System, but Not All Are Persuaded https://www.nytimes.com/2017/03/24/business/dealbook/ubs-trader-fraud-lessons.html
- How a ‘Low Volatility’ Stock Plunged 85% in an Hour (China Huishan Dairy lost $4 billion in value in a flash, after being among the most stable stocks in the world the past 18 months) https://www.wsj.com/articles/how-a-low-volatility-stock-plunged-85-in-an-hour-1490356997
- Theranos Offers Shares for Promise Not to Sue (Blood-testing company’s board approves deal to give investors some of founder Elizabeth Holmes’s personal stake; Murdoch walks away) https://www.wsj.com/articles/theranos-offers-shares-for-promise-not-to-sue-1490301856
- Wells Fargo Digs Deeper Into Its Culture Issues https://www.wsj.com/articles/wells-fargo-digs-deeper-into-its-culture-issues-1490124295
- Former J.P. Morgan Banker Loses Argument in London Whale Case https://www.wsj.com/articles/former-j-p-morgan-banker-loses-argument-in-london-whale-case-1490192615
- Concentration Risks: A Surging Exposure for Risk Managers http://www.brinknews.com/concentration-risks-a-surging-exposure-for-risk-managers/
- The Definition and Risk of Terrorism is Shifting http://www.iii.org/insuranceindustryblog/?p=4875
- R Correlation Tutorial https://www.datacamp.com/community/blog/r-correlation-tutorial
- Bias and variance are two ways of looking at the same thing (Bias is conditional, variance is unconditional) http://andrewgelman.com/2017/03/18/noise-and-bias/
- Andrew Gelman on Social Science, Small Samples, and the Garden of the Forking Paths http://www.econtalk.org/archives/2017/03/andrew_gelman_o.html “One of the challenges of statistical significance is it kind of answers the wrong question. And one way to see that is that when people define it, they tend to get the definition garbled.”
- Some natural solutions to the p-value communication problem—and why they won’t work http://andrewgelman.com/2017/03/21/natural-solutions-p-value-communication-problem-wont-work/
- Why Overlapping Confidence Intervals mean Nothing about Statistical Significance https://medium.com/towards-data-sci...tistical-significance-48360559900a#.brhhc3hiv
- Rookie Currency Traders Are Causing Big Problems https://www.bloomberg.com/news/arti...raders-are-causing-trouble-at-crucial-moments “Tucked deep into a report on foreign-exchange market liquidity was a brief paragraph on how rookie traders could be partly to blame -- along with falling volumes and the growing prevalence of electronic trading -- for the flash crashes that have roiled the $5.1-trillion-a-day currency market over the past two years.”
- Covered Interest Parity http://johnhcochrane.blogspot.com/2017/03/covered-interest-parity.html “The covered interest rate parity relationship fell apart in the financial crisis. And that's understandable. To take advantage of it, you first have to ... borrow dollars. Good luck with that in fall 2008. Long-only investors had more important things on their minds than some cockamaime scheme to invest abroad and use forward markets to gain a half percent per year or so on their abundant (ha!) cash balances. The amazing thing is, the arbitrage spread has not really closed down since the crisis.”
- What makes gambling wrong but insurance right? http://www.bbc.com/news/business-38905963 “The ability to buy derivatives lets companies specialise in a particular market. Otherwise, they would have to diversify - like the Chinese merchants four millennia ago, who didn't want all their goods in one ship. The more an economy specialises, the more it tends to produce. But unlike regular insurance, for derivatives you don't need to find someone with a risk they need to protect themselves against. You just need to find someone willing to take a gamble on any uncertain event anywhere in the world.” [it’s called an insurable interest]
- Why It Matters How We Define Insurance (Some types of insurance charge people according to risk. Others don't. On health care, Americans are caught between the two) http://blogs.wsj.com/economics/2017/03/24/why-it-matters-how-we-define-insurance/ Smart take: "It depends on what you mean by insurance. The basic idea is that a community pools its resources to compensate individuals who suffer some peril such as sickness, death or fire. Pure insurance covers only random perils. Predictable perils generally require higher premiums ... Over time, though, society has increasingly blended subsidies with insurance. Social Security, for example, effectively requires younger, affluent, able-bodied workers and two-earner couples to subsidize older, less affluent and disabled workers and one-earner couples."
- What if breakeven inflation and the “term premium” are measuring the same thing? https://ftalphaville.ft.com/2017/03...he-term-premium-are-measuring-the-same-thing/
- 0% Financing Deals Bite Back Retailers as Fed Raises Rates (Companies will likely absorb the extra cost on no-interest purchases, hoping rate boost is a sign of an improving economy) https://www.wsj.com/articles/fed-ra...ng-deals-more-pricey-for-retailers-1490261405
- A Valeant Update by Professor Aswath Damodaran http://trtl.bz/2mKUmWF Really interesting introspection by one of my favorite value investors
- The Art of (Illiquid) Securities Pricing http://expectedloss.blogspot.in/2017/03/the-art-of-illiquid-securities-pricing.html "Since the crisis, the SEC has ramped up its investigations into pricing issues, and in 2013 set in motion three initiatives (the Financial Reporting and Audit Task Force; the Microcap Fraud Task Force; and the Center for Risk and Quantitative Analytics). There has been a steady and growing stream of findings of asset valuation mismanagement. Some hedge funds have been shut down. (A list of issues here.)"
- Agency Conflicts in Residential Mortgage Securitization: What Does the Empirical Literature Tell Us? https://www.frbatlanta.org/research...esidential-mortgage-securitization-2017-03-21
- Pension Crisis Too Big for Markets to Ignore https://www.bloomberg.com/view/articles/2017-03-24/pension-crisis-too-big-for-markets-to-ignore
- Even San Francisco, Flush With Tech Wealth, Has Pension Problems https://www.bloomberg.com/news/arti...o-flush-with-tech-wealth-has-pension-problems “San Francisco’s net pension liability (a key measure of how much retirement benefits exceed the assets set aside to cover them) more than doubled to $5.5 billion in the year ended in June due to lagging investment returns and an update to assumptions, including longer lifespans for retirees.”
- Blackstone Sends Warning to Illiquid Debt Funds https://www.bloomberg.com/gadfly/ar...kstone-sends-a-warning-to-illiquid-debt-funds “Since the 2008 financial crisis, asset managers have pledged they could both invest in risky, infrequently traded assets while allowing clients to withdraw their money whenever they wanted. This was a supremely attractive feature for investors who had just been stung by a credit seizure that challenged people's faith in "safe" assets. But this structure doesn't work over the long term. It will either lead to lower returns, or, in a worst-case scenario, a complete breakdown.”
- The Future of Family Office Investing (Practical lessons from 3 years of putting capital to work) https://medium.com/startup-grind/the-future-of-family-office-investing-72c594e25c38#.h5vp95irb
- Eton Park to Shut Down as $3 Trillion Hedge Fund Industry Faces Turmoil https://www.nytimes.com/2017/03/23/business/dealbook/eton-park-hedge-fund-closes.html
- Diversification in Multi-Factor Portfolios https://blog.thinknewfound.com/2017/03/diversification-multi-factor-portfolios/
- They Can’t All Be That Smart http://investingresearch.net/2017/03/they-cant-all-be-that-smart/
- Are Factor Investors Getting Paid to Take on Industry Risk? http://beta.morningstar.com/article...rs-getting-paid-to-take-on-industry-risk.html
- High-Frequency Traders Fall on Hard Times (Once-lucrative business is now fighting unfavorable market conditions, brutal competition and rising costs) https://www.wsj.com/articles/high-frequency-traders-fall-on-hard-times-1490092200 “But starting in 2010, the speediest firms began to use microwave networks, shaving milliseconds off the time it takes to transmit information on routes such as the Chicago-New York corridor. Upgrading to microwave networks—and later millimeter-wave and laser technology—added to the costs, traders say. All this hurt HFT firms’ bottom lines just as slumping volatility was eroding their top-line revenues.”
- Rise in new form of portfolio insurance sparks fears https://www.ft.com/content/3eba3f56-08c6-11e7-97d1-5e720a26771b “CTAs, which are also called managed futures funds, are computer-driven vehicles that take advantage of financial markets’ tendency towards momentum. Assets that have gone up tend to go up further, and assets that are falling typically continue to slide. CTAs therefore often automatically bet against an already-falling market, shorting it to profit from further declines, and usually thrive when other strategies are unravelling.”
- A [Bitcoin] Fork in the Road https://vinnylingham.com/a-fork-in-the-road-70288fd3c046#.dbjellbta
- The Need for Very Low Interest Rates in an Era of Subdued Investment Spending http://libertystreeteconomics.newyo...in-an-era-of-subdued-investment-spending.html
- The Global Liquidity Party Is Alive and Well, in Charts https://www.bloomberg.com/news/arti...l-liquidity-party-is-alive-and-well-in-charts
Last edited: