Hello,
I am struggling to find an approach to the following:
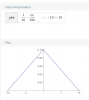
Probability density function of the daily portfolio loss L:
View attachment 2521
How to calculate VaR and Tail VaR with a confidence level of 0.95?
Can someone help please?
Thank you
I am struggling to find an approach to the following:
Probability density function of the daily portfolio loss L:
View attachment 2521
How to calculate VaR and Tail VaR with a confidence level of 0.95?
Can someone help please?
Thank you