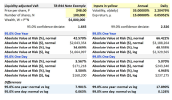
VaR calculation for Example of the LVAR p2.t8 page 6

[JLafr0337]

P2.T8
page 6 (Example of the LVAR)
At the risk of looking stupid here, I'm trying to calculate the VaRs in the table and I can't get the same value as shown in the table

i.e. 95% daily VaR --> 1.645 * 2.20499% = 3.6268% but 3.567% in the table

What am I missing here?

 

[JLafr0337]

Just figured it out, I forgot to account for the return

Correct calculation is: mu - z*sigma --> 0.05952 - 1.645*2.20479

 

[David Harper CFA FRM]

Hi @JLafr0337 Exactly, "Absolute VaR" refers to worst expected loss relative to the initial position and so includes the drift: aVaR = -μ + σ*z. Also, it looks like that exhibit assumes T = 252 trading days. Thanks,

 

[prianthar]

Hi,

When calculating VAR of the book, we take u as negative, but when calculating VAR of the spread, we take u as positive, is this because a larger spread is considered worse or is there another reason MU switches sign in the calc?

 

[David Harper CFA FRM]

Hi @prianthar Yes that is correct. In market risk (what you are calling the book), "absolute VaR" as given by aVaR = -μ + σ*z has the positive drift offsetting the unexpected loss. But in liquidity VaR (LVaR) which adds the liquidity cost--if we are incorporating spread volatility--the "worst expected spread" adds a scaled (multiplied) spread volatility to the mean spread. That's because it's a different measure, but it's totally consistent with VaR: the adverse side of the distribution is a spread widening, not a spread narrowing! Thanks,

 

[prianthar]

Thank you very much. Id rather ask than go there and guess. Appreciated Sir.