Dear All,
I've done all questions and read the chapters assigned, yet there's one thing I cannot get enough clarity on. Tuckman describes 3 models (m1, m1+drift, Ho-Lee), then he makes some interesting points regarding model types (equilibrium and arbitrage-free), and then again gets back to models (Vasicek, lognormal, etc.). However, I cannot find anywhere the cross-reference between model types and described models! For instance, would "Ho-Lee is an arbitrage-free model" be an accurate statement? Vasiscek? m1/m2? etc.
I've done all questions and read the chapters assigned, yet there's one thing I cannot get enough clarity on. Tuckman describes 3 models (m1, m1+drift, Ho-Lee), then he makes some interesting points regarding model types (equilibrium and arbitrage-free), and then again gets back to models (Vasicek, lognormal, etc.). However, I cannot find anywhere the cross-reference between model types and described models! For instance, would "Ho-Lee is an arbitrage-free model" be an accurate statement? Vasiscek? m1/m2? etc.

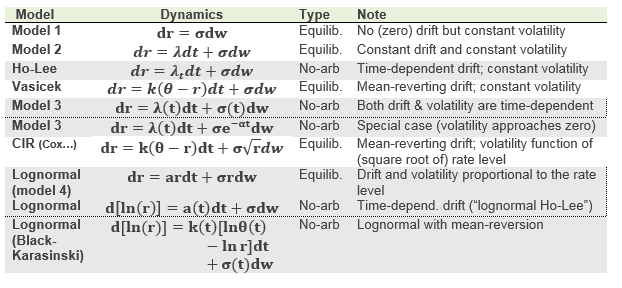
 I was asking myself the same question regarding the Vasicek model. What confuses me a bit now is the following: Does arbitrage-free and no-arbitrage mean the same or is arbitrage-free equal to Equilibrium? I am asking regarding the Practice Question P2.T5.305.3 and Answer A.
I was asking myself the same question regarding the Vasicek model. What confuses me a bit now is the following: Does arbitrage-free and no-arbitrage mean the same or is arbitrage-free equal to Equilibrium? I am asking regarding the Practice Question P2.T5.305.3 and Answer A. ). Thanks!
). Thanks!