Hi @David Harper CFA FRM et al, hope you re having a good weekend. While reviewing below questions, I am struggling to compute PV of payouts and per dollar of premium (bolded). I was trying to sum up the pay out for the year 1 to year 3 and the same thing I did for dollar of premium, but it did not match with what's showing here. Do let me know if you can shed light on this.
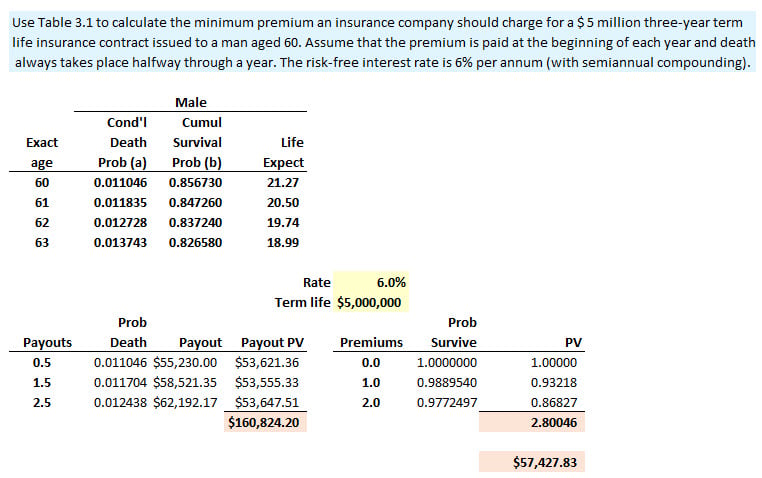
. Question 3.16 Use Table 3.1 to calculate the minimum premium an insurance company should charge for a $5 million three-year term life insurance contract issued to a man aged 60. Assume that the premium is paid at the beginning of each year and death always takes place halfway through a year. The risk-free interest rate is 6% per annum (with semiannual compounding). Answers: The unconditional probability of the man dying in years one, two, and three can be calculated from Table 3.1 as follows: Year 1: 0.011046 Year 2: (1−0.011046) × 0.011835 = 0.011704 Year 3: (1−0.011046) × (1−0.011835) × 0.012728 = 0.012438 The expected payouts at times 0.5, 1.5, 2.5 are therefore $55,230.00, $58,521.35, and $62,192.17. These have a present value of $160,824.20. The survival probability of the man is Year 0: 1 Year 1: 1−0.011046 = 0.988594 Year 2: 1−0.011046−0.011704 = 0.97725 The present value of the premiums received per dollar of premium paid per year is therefore 2.800458. The minimum premium is 160,824.20/ 2.800458 = 57,427.83 or $57,427.
. Question 3.16 Use Table 3.1 to calculate the minimum premium an insurance company should charge for a $5 million three-year term life insurance contract issued to a man aged 60. Assume that the premium is paid at the beginning of each year and death always takes place halfway through a year. The risk-free interest rate is 6% per annum (with semiannual compounding). Answers: The unconditional probability of the man dying in years one, two, and three can be calculated from Table 3.1 as follows: Year 1: 0.011046 Year 2: (1−0.011046) × 0.011835 = 0.011704 Year 3: (1−0.011046) × (1−0.011835) × 0.012728 = 0.012438 The expected payouts at times 0.5, 1.5, 2.5 are therefore $55,230.00, $58,521.35, and $62,192.17. These have a present value of $160,824.20. The survival probability of the man is Year 0: 1 Year 1: 1−0.011046 = 0.988594 Year 2: 1−0.011046−0.011704 = 0.97725 The present value of the premiums received per dollar of premium paid per year is therefore 2.800458. The minimum premium is 160,824.20/ 2.800458 = 57,427.83 or $57,427.
but I hope you had a good weekend! I entered this EOC Q&A into a modified version of our XLS sheet. Here is the sheet I just created if you want to take a closer look 
