YouTube T1-6 What is bootstrap historical simulation?

[Nicole Seaman]

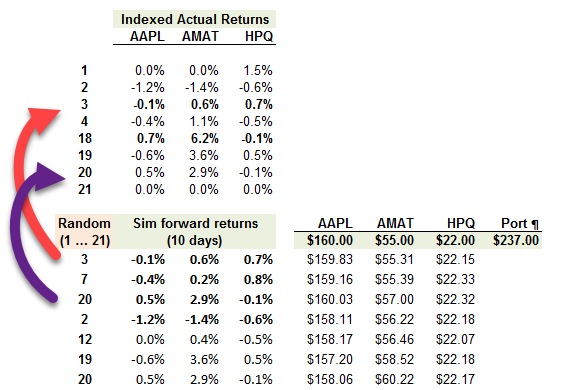
The key idea of Boostrap HS is "sampling with replacement:" we randomly retrieve ACTUAL daily returns and use them to simulate forward.

Here is David's XLS: http://trtl.bz/2yzTYPM

 

[Lenka2019]

I didn't understand where those Sim forward returns come from. For index 1,2,3,4,18,19,20,21, we can look back and find them in historical window by using the VLOOKUP, but how to generate forward returns for other random values, I am still confused about it.

 

[David Harper CFA FRM]

Hi @Lenka2019 In this bootstrap HS, we have a historical window of indexed returns, see below; e.g., the day 3 returns were actually AAPL = -1.2%, AMAT = -1.4%, HPQ = -0.6%. So we have an indexed, actual returns; day 20 was AAPL = 0.5%, AMAT = 2.9%, HPQ = -0.1%. Then the simulation simply needs a random number going forward, 1:n where n = the number of actual indexed days, so we are randomly selecting a day in the past window. My excel uses =INT(RAND()*21)+1 to retrieve a random integer from 1 to 21 because i only have 21 days in the actual history. My first random number was 3, so i retrieve those returns (red arrow) and apply the returns to the current portfolio.

In GARP's VRM Chapter 2, they illustrate only a historical simulation (as opposed to this bootstrap HS). The difference is that their (simple) HS does not retrieve a random(ly indexed) day; rather, their first day would apply the returns from the first day, second day would apply returns to the second day, etc ... I hope that's helpful!

 

[Rblc]

@David Harper CFA FRM Hi David, my apologies for the stupid inquiry but in the first example you give in your video (and in Garp example above) we assume equal weights . Does this mean(we assume) the underlying distribution for the stock price is a uniform distribution ?

 

[David Harper CFA FRM]

HI @RajivBoolell Not stupid, thought provoking! It is true that the randomization is random discrete uniform variable; e.g., if there is a history of 21 daily returns, then the probability of selecting a specific historical day is 1/21. But this reflects our want to conduct a genuinely random sample (see https://en.wikipedia.org/wiki/Simple_random_sample ... "In statistics, a simple random sample is a subset of individuals (a sample) chosen from a larger set (a population). Each individual is chosen randomly and entirely by chance, such that each individual has the same probability of being chosen at any stage during the sampling process, and each subset of k individuals has the same probability of being chosen for the sample as any other subset of k individuals")

By randomizing a uniform discrete variable as the basis for selection we are ensuring that our sample (as the size increases) is representative of the population, which in this case, each day does have an equal weight in the actual history (although history is a sample of the unknown population such that bootstrapping is re-sampling: taking several samples of a single sample). If the "true" (unseen) population returns are normal, then we can expect the historical sample (of daily returns) to be approximately or roughly normal, and a random re-sampling (bootstrapping) selects the actual days based on uniform random discrete, but that's just "being random," such that we should expect the re-sample to also be roughly normal (size depending).

So i don't think the uniform random variable, as a basis for selection, is imposing any expectation on the underlying stock price distribution. I think it's ensuring a representative re-sample. Although i am not highly confident that I've I nailed the statistical property, frankly, because it raises an interesting question: if we alter to a non-uniform random variable, which properties do we distort ...

I would add that this simple HS is just one approach. Another is filtered historical simulation: however, the bootstrap step in FHS also re-samples by giving each standardized, day an equal probability of being selected (ie, random uniform discrete). The issues that typically are related to cross-correlation (that correlation among stock returns on a given day, which bootstrapping does maintain because it selects the day's vector of returns) and correlation over time (aka, auto-correlation, which simple HS does not maintain because it conducts an i.i.d. random sample of the historical days). I hope that's helpful .. not stupid, thought provoking to me!

 

[LisaCoy]

Wow this is extremely well articulated and helpful. Not to mention well made. Thanks a ton!