emilioalzamora1
Well-Known Member
Dear All, Dear @David Harper CFA FRM,
first, apologies if this turns out to be a quick fix/straightfoward problem but I do need some help/input with regard to the following:
This is from the CAIA (level 2) and it's about a 3-asset (classes) example of risk budgeting.
You are given the means of the 3 assets and their respective weights as well as variance-covariance matrix.
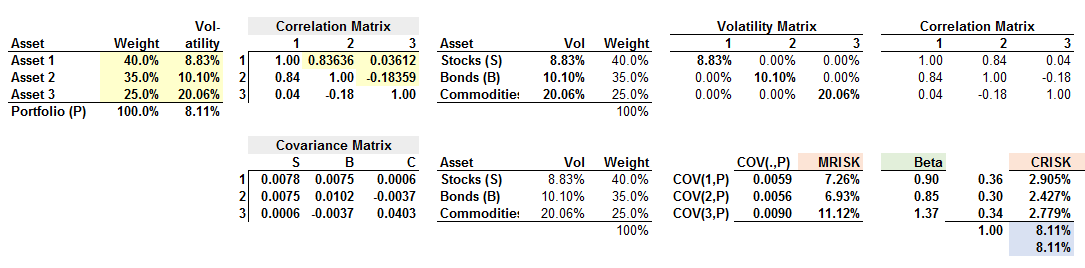
Asset (1): mu = 10% (weight 40%), variance = 0.0078
Asset (2): mu = 12% (weight 35%), variance = 0.01020
Asset (3): mu = 4% (weight 25%), variance = 0.04025
covariance (1,2) = 0.00746
covariance (1,3) = 0.00064
covariance (2,3) = -0.00372
Based on this we can simply calculate the variance of the 3-asset portfolio having:
sigma^2 (portfolio) = (0.4^2 * 0.0078) + (0.35^2 * 0.01020) + (0.25^2 * 0.04025) + (2*0.4*0.35*0.00746) + (2*0.4*0.25*0.00064) + (2*0.35*0.25*-0.00372) = 0.006578925 >>>> sigma (portfolio) = 0.08111 >>>> 8.11%
The question troubling me now is the fact how the contribution of each asset is calculated.
The CAIA uses the following formula for the risk contribution of each asset:
∂sigma(p)/∂ w(asset 1) * weight(asset 1) = cov(asset 1, portfolio)/sigma(p) * weight(asset 1) = ρ(asset 1, portfolio) * sigma (asset 1) * weight(asset 1)
This would imply that need to compute the covariance of asset 1 with the portfolio. But, how can this be done without having the correlation coefficient?
It says that the contribution of Asset 1 = ρ(asset 1, portfolio) * sigma (asset 1) * weight(asset 1)
where the value for ρ(asset 1, portfolio) * sigma (asset 1) is 7.26%.
In other words, we need to find the correl coeffcient between asset 1 and the portfolio to get 7.26%.
The total risk contribution amounts then: 7.26% * 40%
Any input is highly appreciated!
[The theory behind this is discussed in much more detail in Fabozzi 'Robust Portfolio Optimization and Management']
first, apologies if this turns out to be a quick fix/straightfoward problem but I do need some help/input with regard to the following:
This is from the CAIA (level 2) and it's about a 3-asset (classes) example of risk budgeting.
You are given the means of the 3 assets and their respective weights as well as variance-covariance matrix.
Asset (1): mu = 10% (weight 40%), variance = 0.0078
Asset (2): mu = 12% (weight 35%), variance = 0.01020
Asset (3): mu = 4% (weight 25%), variance = 0.04025
covariance (1,2) = 0.00746
covariance (1,3) = 0.00064
covariance (2,3) = -0.00372
Based on this we can simply calculate the variance of the 3-asset portfolio having:
sigma^2 (portfolio) = (0.4^2 * 0.0078) + (0.35^2 * 0.01020) + (0.25^2 * 0.04025) + (2*0.4*0.35*0.00746) + (2*0.4*0.25*0.00064) + (2*0.35*0.25*-0.00372) = 0.006578925 >>>> sigma (portfolio) = 0.08111 >>>> 8.11%
The question troubling me now is the fact how the contribution of each asset is calculated.
The CAIA uses the following formula for the risk contribution of each asset:
∂sigma(p)/∂ w(asset 1) * weight(asset 1) = cov(asset 1, portfolio)/sigma(p) * weight(asset 1) = ρ(asset 1, portfolio) * sigma (asset 1) * weight(asset 1)
This would imply that need to compute the covariance of asset 1 with the portfolio. But, how can this be done without having the correlation coefficient?
It says that the contribution of Asset 1 = ρ(asset 1, portfolio) * sigma (asset 1) * weight(asset 1)
where the value for ρ(asset 1, portfolio) * sigma (asset 1) is 7.26%.
In other words, we need to find the correl coeffcient between asset 1 and the portfolio to get 7.26%.
The total risk contribution amounts then: 7.26% * 40%
Any input is highly appreciated!
[The theory behind this is discussed in much more detail in Fabozzi 'Robust Portfolio Optimization and Management']
Last edited: