gargi.adhikari
Active Member
In reference to R19.P1.T3.Hull-Chapter 6: Topic-Extract LIBOR Zero Rates:-
Rf ( T2-T1) = [ R2T2- R1T1 ]
=> R2 = [ Rf ( T2-T1) + R1T1 ] / T2
To calculate the last Zero-Rate, we did the following:-
4.994% = [ 491 * 4.893% + 5.5 % ( 589- 491) ] / 589
Based on the Zero Rate and Forward Rate calculations in other chapters, should we not have used 5.6% = as Rf , instead of the prior period's Rf= 5.5 % ...?
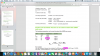
Rf ( T2-T1) = [ R2T2- R1T1 ]
=> R2 = [ Rf ( T2-T1) + R1T1 ] / T2
To calculate the last Zero-Rate, we did the following:-
4.994% = [ 491 * 4.893% + 5.5 % ( 589- 491) ] / 589
Based on the Zero Rate and Forward Rate calculations in other chapters, should we not have used 5.6% = as Rf , instead of the prior period's Rf= 5.5 % ...?




