You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
R19.P1.T3.FIN_PRODS_HULL_Ch10_American_Options_Pull-Call-Parity-Relationship
- Thread starter gargi.adhikari
- Start date
Hi @gargi.adhikari That derivation happens to be an end of chapter (EOC) question in Hull, and we do include Hull's EOC Q&A (thanks to @Nicole Seaman !) as addendums to our own practice questions, in the PQ document. So you will find the solution (i.e., the derivation to this American style put-call quasi-parity, I will call it!) on page 300 - 301 of the associated PQ set at https://learn.bionicturtle.com/topic/question-set-hull-chapters-1-2-3-4-5-6-7-10-11-12-26/ ... I can see it solves both sides. On the one side, he (Hull because to be honest, I'm not sure I would be able to solve this quickly on my one) simply asserts European put-call parity:
- p = c + K*exp(-rT) - S(0); then he replaces (p) and (c) with, respectively, P ≥ p, and c = C. The first, that an American put must be equal to or greater than a European put, P ≥ p, never seems to give folks a problem because of course the additional ability to exercise early could only add value (an American-style option can be viewed as an option with an additional option to exercise early). However, the use of c = C has caused some discussion/disagreement here in the forum in previous years. Hull's rationale is "Because American call options are never exercised early when there are no dividends, they are equivalent to European call options, so that C = c." This view, in my paraphrase is something like: the early exercise feature should never be used, therefore it adds no value in addition to the European option (I'm not saying I agree with this ...). Okay but if we accept those two equalities, then:
- Due to P ≥ p: P ≥ c + K*exp(-rT) - S(0), and then
- Due to c = C: P ≥ C + K*exp(-rT) - S(0), so that:
- P - C ≥ K*exp(-rT) - S(0), and multiplying both sides by (-1):
- C-P ≤ S(0) - K*exp(-rT), which is one side/half of the equation, yay!

- Due to P ≥ p: P ≥ c + K*exp(-rT) - S(0), and then
- I will refer you to page 300 for the other side, because to be honest, I haven't reviewed it...
 I hope that's helpful!
I hope that's helpful!
Last edited:
gargi.adhikari
Active Member
@David Harper CFA FRM Thank you so much -as always for coming to the rescue 

@gargi.adhikari sure thing, I view *every* question as an opportunity to learn something! e.g., I decided to give this a name: put-call quasi-parity ... hopefully that's a new phrase, it's a small innovation but maybe i will trademark it and somehow issue some digital (ICO) tokens to monetize it?! #teasing
gargi.adhikari
Active Member
@David Harper CFA FRM That sure sounds like good idea to me ..lol... 

Hi there, to complete the cycle,
Proof of the LHS as I understand it:
Normal Put Call Parity:
c+K*exp(-rf*t) = p + S
This is assuming we have a portfolio of one Long European Call(c), PV of Strike price as Cash, Short European Put (p) and Short one Share. Here the options are all European.
Now, replicate the same portfolio, this time using American options, therefore, our portfolio becomes:
1. Long one American Call (C)
2. Short one American Put (P)
3. Short one Share
4. Keep K itself, rather than the PV of K as Cash
It can be proved retrospectively that:
c+K*exp(-rf*t)-p-S = 0
c+K - p - S >= 0 and as c = C, C+K - p - S >= 0 which finally leads to C+K - P - S >= 0 which leads to C-P >= S-K
Now, there are two cases, as the American Puts alone can be exercised before maturity, we can have a case where they are and a case where they aren't
Case A: American Puts exercised prior to maturity
Case B: American Puts Held till Maturity
Case B(1) : Where the Call is exercised at maturity
Case B(2): Where the Call lapses and the Put is exercised
Case A: Where the American Puts are exercised at a time t prior to maturity T, the value of the call remains at what it is at that point in timeand I assume that as the cash K is kept idle, its value reduces by the time value of money as we do not invest the K at the rf rate. We can assume that the Cash is invested at Rf rate, in which case, it becomes K*exp(rf*t)
C(t) + K*exp(rf*t) - (K-S(t)) - S(t)
C(t) + K*exp(rf*t) - K >=0,
Case B(1)
If the Call is exercised, it means that S>K and the value of the Put becomes 0
S(T) -K + K *exp(rf*T) - 0 - S(T)
Thus, K*exp(rf*T) - K which is again >= 0
Case B(2)
The Call lapses and the Put is exercised at maturity as K>S
0+K*exp(rf*T) - [K-S(T)]-S(T), which is K*exp(rf*T)-K which >= 0, note that there is an equality in B(1) and B(2)
Thus the entire Portfolio becomes:
C+K-P-S >= 0 in all situations
C-P>=S-K which is the LHS of the "Put Call Quasi Parity" in the words of the great @David Harper CFA FRM
I hope David, my understanding is correct.
For more info, people may refer this paper by NYU: http://www.math.nyu.edu/~cai/Courses/Derivatives/lecture8.pdf
EDIT: Used just the compounding condition and replaced the exp(-rf*t)
Proof of the LHS as I understand it:
Normal Put Call Parity:
c+K*exp(-rf*t) = p + S
This is assuming we have a portfolio of one Long European Call(c), PV of Strike price as Cash, Short European Put (p) and Short one Share. Here the options are all European.
Now, replicate the same portfolio, this time using American options, therefore, our portfolio becomes:
1. Long one American Call (C)
2. Short one American Put (P)
3. Short one Share
4. Keep K itself, rather than the PV of K as Cash
It can be proved retrospectively that:
c+K*exp(-rf*t)-p-S = 0
c+K - p - S >= 0 and as c = C, C+K - p - S >= 0 which finally leads to C+K - P - S >= 0 which leads to C-P >= S-K
Now, there are two cases, as the American Puts alone can be exercised before maturity, we can have a case where they are and a case where they aren't
Case A: American Puts exercised prior to maturity
Case B: American Puts Held till Maturity
Case B(1) : Where the Call is exercised at maturity
Case B(2): Where the Call lapses and the Put is exercised
Case A: Where the American Puts are exercised at a time t prior to maturity T, the value of the call remains at what it is at that point in time
C(t) + K*exp(rf*t) - (K-S(t)) - S(t)
C(t) + K*exp(rf*t) - K >=0,
Case B(1)
If the Call is exercised, it means that S>K and the value of the Put becomes 0
S(T) -K + K *exp(rf*T) - 0 - S(T)
Thus, K*exp(rf*T) - K which is again >= 0
Case B(2)
The Call lapses and the Put is exercised at maturity as K>S
0+K*exp(rf*T) - [K-S(T)]-S(T), which is K*exp(rf*T)-K which >= 0, note that there is an equality in B(1) and B(2)
Thus the entire Portfolio becomes:
C+K-P-S >= 0 in all situations
C-P>=S-K which is the LHS of the "Put Call Quasi Parity" in the words of the great @David Harper CFA FRM

I hope David, my understanding is correct.
For more info, people may refer this paper by NYU: http://www.math.nyu.edu/~cai/Courses/Derivatives/lecture8.pdf
EDIT: Used just the compounding condition and replaced the exp(-rf*t)
Last edited:
gargi.adhikari
Active Member
@QuantMan2318 Thank u so much....salute to the great ones like u and the one and only @David Harper CFA FRM ....RESPECT 

gargi.adhikari
Active Member
@David Harper CFA FRM
I just wanted to double check/confirm the direction of the inequality for the " Put-Call Quasi-Parity" for American Options....( btw... I just used your newly coined term...hope you get royalties in your bitcoin account ...lol...) The direction of the inequality below should be reverse...?....thinking it's a typo...but just to make sure I did not miss anything...wanted to confirm ...Thanks for patiently answering my questions....
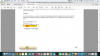
I just wanted to double check/confirm the direction of the inequality for the " Put-Call Quasi-Parity" for American Options....( btw... I just used your newly coined term...hope you get royalties in your bitcoin account ...lol...) The direction of the inequality below should be reverse...?....thinking it's a typo...but just to make sure I did not miss anything...wanted to confirm ...Thanks for patiently answering my questions....

Hi @gargi.adhikari Oh, I accept bitcoin!  (I bought a little bitcoin a couple of years ago, but I should have bought a lot. Darn!!!) Yes, you look to be correct, that appears to be our typo in the proof, sorry. Above, when I got to:
(I bought a little bitcoin a couple of years ago, but I should have bought a lot. Darn!!!) Yes, you look to be correct, that appears to be our typo in the proof, sorry. Above, when I got to:
 (I bought a little bitcoin a couple of years ago, but I should have bought a lot. Darn!!!) Yes, you look to be correct, that appears to be our typo in the proof, sorry. Above, when I got to:
(I bought a little bitcoin a couple of years ago, but I should have bought a lot. Darn!!!) Yes, you look to be correct, that appears to be our typo in the proof, sorry. Above, when I got to:- P - C ≥ K*exp(-rT) - S(0); at this point, in my forum post above (not page 300 of the PQ document that you are showing) I multiplied each side by (-1) which implies:
- C-P ≤ S(0) - K*exp(-rT) ... because if x > y then -x < -y; e.g., if 4 > 3, then -4 < -3 ... and to get from (P-C) to (C-P), you need to multiply by -1 .... Thank you (again again) for your attention to detail!
 (cc @Nicole Seaman I noted this in wrike as part of our non-urgent accumulation...)
(cc @Nicole Seaman I noted this in wrike as part of our non-urgent accumulation...)
gargi.adhikari
Active Member
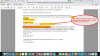
@David Harper CFA FRM ...I have a follow up question on the Put_Call_Quasi_Parity...( cha hing ..lol.. )(S - K) <= (C - P ) <= ( S - Ke^ -rt)
If K is NOT invested at Rf and it’s value reduces by Rf , so that we have: PF -I' worth Max(St,K) -K[ 1- EXP(- rT) ] which would always be LESS THAN Max(St,K) which in turn is the value of Portfolio 'J' So (P +S) >=( C +K ) => (C-P) <= (S-K)...so am having trouble with the LHS of the Put_Call_Quasi_Parity... :-(
I have the same problem in @QuantMan2318 's derivation above with the LHS....
In @QuantMan2318 's derivation - Case A : where K is not invested and it's value goes down by Rf, we have:-
{Ct + K* EXP(-Rf *T) } - [ {K - St } + St ] => {Ct + K* EXP(-Rf *T) } - K => [ { ( St - K* EXP(-Rf*T) ) } + {K* EXP(-Rf *T) } - K} ] as Ct = ( St - K* EXP(-Rf*T) )
Therefore we have, the above as ( St -K ) as the +ve and -ve K* EXP(-Rf*T) cancel out... now whenever St < K , (St -K) would be <0
That is {Ct + K* EXP(-Rf *T) } - [ {K - St } + St ] or ( C+ K) - ( P +S) < 0 => So, (C-P) <= ( S-K) instead of (C-P) > = ( S-K)
What am I getting wrong here... ? :-( :-(
If K is NOT invested at Rf and it’s value reduces by Rf , so that we have: PF -I' worth Max(St,K) -K[ 1- EXP(- rT) ] which would always be LESS THAN Max(St,K) which in turn is the value of Portfolio 'J' So (P +S) >=( C +K ) => (C-P) <= (S-K)...so am having trouble with the LHS of the Put_Call_Quasi_Parity... :-(
I have the same problem in @QuantMan2318 's derivation above with the LHS....
In @QuantMan2318 's derivation - Case A : where K is not invested and it's value goes down by Rf, we have:-
{Ct + K* EXP(-Rf *T) } - [ {K - St } + St ] => {Ct + K* EXP(-Rf *T) } - K => [ { ( St - K* EXP(-Rf*T) ) } + {K* EXP(-Rf *T) } - K} ] as Ct = ( St - K* EXP(-Rf*T) )
Therefore we have, the above as ( St -K ) as the +ve and -ve K* EXP(-Rf*T) cancel out... now whenever St < K , (St -K) would be <0
That is {Ct + K* EXP(-Rf *T) } - [ {K - St } + St ] or ( C+ K) - ( P +S) < 0 => So, (C-P) <= ( S-K) instead of (C-P) > = ( S-K)
What am I getting wrong here... ? :-( :-(

I have the same problem in @QuantMan2318 's derivation above with the LHS....
In @QuantMan2318 's derivation - Case A : where K is not invested and it's value goes down by Rf, we have:-
{Ct + K* EXP(-Rf *T) } - [ {K - St } + St ] => {Ct + K* EXP(-Rf *T) } - K => [ { ( St - K* EXP(-Rf*T) ) } + {K* EXP(-Rf *T) } - K} ] as Ct = ( St - K* EXP(-Rf*T) )
Therefore we have, the above as ( St -K ) as the +ve and -ve K* EXP(-Rf*T) cancel out... now whenever St < K , (St -K) would be <0
That is {Ct + K* EXP(-Rf *T) } - [ {K - St } + St ] or ( C+ K) - ( P +S) < 0 => So, (C-P) <= ( S-K) instead of (C-P) > = ( S-K)
What am I getting wrong here... ? :-( :-(
I need some time for having a look at Hull's derivation, however, I can answer your second point. You have taken my case A. In that situation, the Call option neither lapses nor is it exercised and hence it is just a known quantity with some positive value > 0, So we should not replace C with S(t) - K*exp(-rf*t). We can see that the American Call is assumed to be the same as the European Call and hence it will have some value till maturity (at-least the time value if not the intrinsic value at the time the American Put is exercised)
We have to remember that Case A is unique in that we are exercising the American Put prior to Maturity of the Option
Even if you assume the portfolio contained an European Call as opposed to an American Call, it will never be exercised (or lapse) prior to maturity and hence will have some value till the maturity of the option
Hope this helped
Thanks
gargi.adhikari
Active Member
@QuantMan2318 Thanks so much for your response.... 
Am still Fuzzy on the LHS.... my apologies... :-( :-(
So in Case A, say the St< K and so the Call does not get exercised neither it lapses. So we have :-
C(t) + K*exp(-rf*t) - K >=0 -->[ C(t) -K { 1- exp(-rf*t) } ] . Now, exp(-rf*t) is always LESS THAN 1. So, { 1- exp(-rf*t) } = +ve and LESS THAN 1. So, K { 1- exp(-rf*t) } is some +ve number < K
So, if the Strike Price is such that, K { 1- exp(-rf*t) } > C(t) , then :-[ C(t) + K*exp(-rf*t) - K ] would be LESS THAN 0 .... :-( ...?

Am still Fuzzy on the LHS.... my apologies... :-( :-(
So in Case A, say the St< K and so the Call does not get exercised neither it lapses. So we have :-
C(t) + K*exp(-rf*t) - K >=0 -->[ C(t) -K { 1- exp(-rf*t) } ] . Now, exp(-rf*t) is always LESS THAN 1. So, { 1- exp(-rf*t) } = +ve and LESS THAN 1. So, K { 1- exp(-rf*t) } is some +ve number < K
So, if the Strike Price is such that, K { 1- exp(-rf*t) } > C(t) , then :-[ C(t) + K*exp(-rf*t) - K ] would be LESS THAN 0 .... :-( ...?
@QuantMan2318 Thanks so much for your response....
Am still Fuzzy on the LHS.... my apologies... :-( :-(
So in Case A, say the St< K and so the Call does not get exercised neither it lapses. So we have :-
C(t) + K*exp(-rf*t) - K >=0 -->[ C(t) -K { 1- exp(-rf*t) } ] . Now, exp(-rf*t) is always LESS THAN 1. So, { 1- exp(-rf*t) } = +ve and LESS THAN 1. So, K { 1- exp(-rf*t) } is some +ve number < K
So, if the Strike Price is such that, K { 1- exp(-rf*t) } > C(t) , then :-[ C(t) + K*exp(-rf*t) - K ] would be LESS THAN 0 .... :-( ...?
Thanks for asking me these probing questions, if not for you, I would never have realized that I was making a mistake by including both discounting and compounding in the same angle
 . To make it clear, the equation only works if you invest in the Rf rate. Therefore, we have to invest in Rf rate only where we have K*exp(rf*t).
. To make it clear, the equation only works if you invest in the Rf rate. Therefore, we have to invest in Rf rate only where we have K*exp(rf*t).I am sorry, I got confused w.r.t the notation used in the NYU paper. Just use the K*exp(rf*t). While, going through the paper, I found out that they had used my investment at Rf rate as B(0,1)^-1 which I had wrongly assumed to be discounting. Now that I realize it, your logic points out the flaw in B(1) and B(2) as well, the inequality holds only in the case of compounding. I apologize for this gaffe

However, please do note that my earlier point of not exercising the European option while you exercise the American option still applies and it will be a positive quantity C(t)
I hope @David Harper CFA FRM, you will excuse me for this error. I have also taken the liberty of modifying the above derivation to include only the compounding and am excluding the discounting from the same.
Thanks
Last edited:
@David Harper CFA FRM ...I have a follow up question on the Put_Call_Quasi_Parity...( cha hing ..lol.. )(S - K) <= (C - P ) <= ( S - Ke^ -rt)
If K is NOT invested at Rf and it’s value reduces by Rf , so that we have: PF -I' worth Max(St,K) -K[ 1- EXP(- rT) ] which would always be LESS THAN Max(St,K) which in turn is the value of Portfolio 'J' So (P +S) >=( C +K ) => (C-P) <= (S-K)...so am having trouble with the LHS of the Put_Call_Quasi_Parity... :-(
I think this question doesn't arise at all now
 . We only invest at Rf rate and hence Hull's derivation is also proved.
. We only invest at Rf rate and hence Hull's derivation is also proved.Thanks
gargi.adhikari
Active Member
@QuantMan2318 Thanks so much for elaborately laying out each possible scenario in this proof..also a big thank you for taking the time to confirm not considering the scenario of 'K' not getting invested...the rest works out perfectly ! Again thanks for the detailed scenarios..very grateful to the very knowledgable members on this forum like you @QuantMan2318 and @ShaktiRathore and many others and of course the GURU HIMSELF - @David Harper CFA FRM  who so patiently answers our ignorant questions...cannot thank u all for your patience with us..
who so patiently answers our ignorant questions...cannot thank u all for your patience with us.. 
 who so patiently answers our ignorant questions...cannot thank u all for your patience with us..
who so patiently answers our ignorant questions...cannot thank u all for your patience with us.. 
Last edited:
Similar threads
- Replies
- 0
- Views
- 206
- Replies
- 0
- Views
- 851
- Replies
- 0
- Views
- 822
- Replies
- 0
- Views
- 696