gargi.adhikari
Active Member
In Reference to R15.P1.T2.DIEBOLD_CH7_Topic: WOLD'S_REPRESENTATION & COVARIANT-STATIONARY :-
In Diebold Ch-7: On Pg 20 we have a statement stating the following:
The " Non-Stationary Components " such as "Trends & Seasonality" should be removed from a Time Series to ultimately form a Covariance-Stationary-Series.
But then On Pg 24: (2nd Screenshot) We have the following statement for Wold's Theorem..
" We really need an appropriate model for “what’s left” after fitting the Trend and Seasonal components; i.e., a model for a Covariance-Stationary Residual
My Question is that, don't we "Remove" the Trend and Seasonal Components and Not "Fit" them into the Model...am I understanding this correctly..? Appreciate and thankful for sharing insights on this.
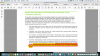
In Diebold Ch-7: On Pg 20 we have a statement stating the following:
The " Non-Stationary Components " such as "Trends & Seasonality" should be removed from a Time Series to ultimately form a Covariance-Stationary-Series.
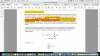
But then On Pg 24: (2nd Screenshot) We have the following statement for Wold's Theorem..
" We really need an appropriate model for “what’s left” after fitting the Trend and Seasonal components; i.e., a model for a Covariance-Stationary Residual
My Question is that, don't we "Remove" the Trend and Seasonal Components and Not "Fit" them into the Model...am I understanding this correctly..? Appreciate and thankful for sharing insights on this.