You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
R10.P1.T1.BODIE_CH10_Portfoloio_Arbitrage_SML
- Thread starter gargi.adhikari
- Start date
-
- Tags
- bodie portfolio-arbitrage
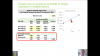
Hi @gargi.adhikari I borrowed that example directly from Bodie (i am not very original!  ). I hope I spoke to this, but the arbitrage portfolio = 50% security A + 50% the riskfree asset. It's β = 50%*1.0 + 50%*0 = 0.50, because the risk-free asset has a beta of zero, right? (it's correlation with the market factor is zero, so its beta is also zero). Similarly, the expected return = 50%*10% + 50% *4.0% = +7.0%. This is the achievement of an arbitrage opportunity in the single-factor world because we have Security C and the Portfolio (security A + Rf free rate) that have the same beta but different returns, so we can short Security C and buy the Portfolio with neutral net beta yet +1.0% return. I hope that answers it! Thanks,
). I hope I spoke to this, but the arbitrage portfolio = 50% security A + 50% the riskfree asset. It's β = 50%*1.0 + 50%*0 = 0.50, because the risk-free asset has a beta of zero, right? (it's correlation with the market factor is zero, so its beta is also zero). Similarly, the expected return = 50%*10% + 50% *4.0% = +7.0%. This is the achievement of an arbitrage opportunity in the single-factor world because we have Security C and the Portfolio (security A + Rf free rate) that have the same beta but different returns, so we can short Security C and buy the Portfolio with neutral net beta yet +1.0% return. I hope that answers it! Thanks,
 ). I hope I spoke to this, but the arbitrage portfolio = 50% security A + 50% the riskfree asset. It's β = 50%*1.0 + 50%*0 = 0.50, because the risk-free asset has a beta of zero, right? (it's correlation with the market factor is zero, so its beta is also zero). Similarly, the expected return = 50%*10% + 50% *4.0% = +7.0%. This is the achievement of an arbitrage opportunity in the single-factor world because we have Security C and the Portfolio (security A + Rf free rate) that have the same beta but different returns, so we can short Security C and buy the Portfolio with neutral net beta yet +1.0% return. I hope that answers it! Thanks,
). I hope I spoke to this, but the arbitrage portfolio = 50% security A + 50% the riskfree asset. It's β = 50%*1.0 + 50%*0 = 0.50, because the risk-free asset has a beta of zero, right? (it's correlation with the market factor is zero, so its beta is also zero). Similarly, the expected return = 50%*10% + 50% *4.0% = +7.0%. This is the achievement of an arbitrage opportunity in the single-factor world because we have Security C and the Portfolio (security A + Rf free rate) that have the same beta but different returns, so we can short Security C and buy the Portfolio with neutral net beta yet +1.0% return. I hope that answers it! Thanks,gargi.adhikari
Active Member
@David Harper CFA FRM Thanks so much for the clarification on this - very clear now 



 .....One lingering question on this....did we choose the 50 %-50% weightage of the Security A & the Risk Free Asset for some specific reason..?
.....One lingering question on this....did we choose the 50 %-50% weightage of the Security A & the Risk Free Asset for some specific reason..?




 .....One lingering question on this....did we choose the 50 %-50% weightage of the Security A & the Risk Free Asset for some specific reason..?
.....One lingering question on this....did we choose the 50 %-50% weightage of the Security A & the Risk Free Asset for some specific reason..?@gargi.adhikari if you look at the SML, security C is below the line so it is mispriced and we can arbitrage if we buy the portfolio on the line (vertically above it) with the same beta, which is 0.50. So its because (C) has beta of 0.5 and we want an "efficient" portfolio with beta = 0.5. The easiest way to achieve this is mix in 50% Rf with Security (A). Thanks,
gargi.adhikari
Active Member
@David Harper CFA FRM Thanks so much- am good with the Arbitrage Portfolio being .5...still a bit foggy though on why we chose the Weight of the Risky Portfolio to be 50% and not some other weight...60%, 70% ...etc...
@gargi.adhikari it starts with identifying Security C as mispriced (below the line); it's return of 6.0% is too low. The arbitrage wants a portfolio on the line with beta = 0.5 to match the beta of (C). We are matching the beta of the mispriced security. There will usually be more than one way to get this, but the easiest is to notice that (A) is twice the beta, so if we mix 50% of Rf, we will match the beta. Because we are going to short (C) and long the portfolio to neutralize beta (beta = 0) but the expected return is +1.0% on a zero-beta portfolio. If the single factor applies, whatever happens we gain + 1.0% because their betas are equal. An arbitrage is riskless profit, if we end up non zero beta there will still be risk. Thanks,
gargi.adhikari
Active Member
Got It ! @David Harper CFA FRM Thanks so much !!
Similar threads
- Replies
- 1
- Views
- 515
- Replies
- 2
- Views
- 616
- Replies
- 0
- Views
- 296
- Replies
- 0
- Views
- 176