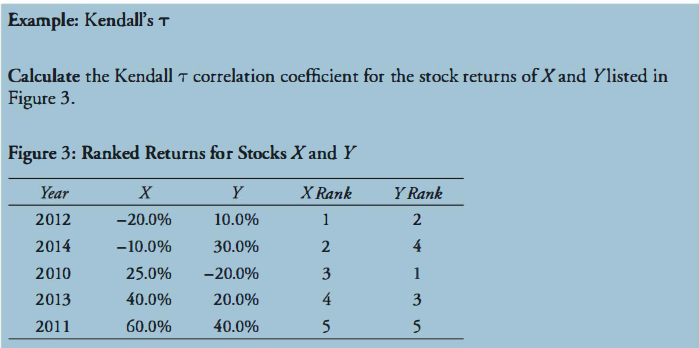
I wrote to Meissner (I don't see an errata yet for his new book, which is excellent) that I think the example for (3.2.3) Kendall's tau is incorrect. He shows five (x,y) pairs. Five (X,Y) sets implies 10 pairs (of X,Y pairs). 10 is the "triangle number" for 4 = (n-5), see http://en.wikipedia.org/wiki/Triangular_number; i.e., there are 10 pairs in the upper/lower matrix not including the diagonal. If you see the triangle, then n*(n-1)/2 will make sense! I love triangle numbers, I think I first encountered them in second grade and that's about the time I fell in love with math ...
My XLS is here https://www.dropbox.com/s/1f510upcpnp7ide/MR-9-kendalls-tau.xlsx?dl=0
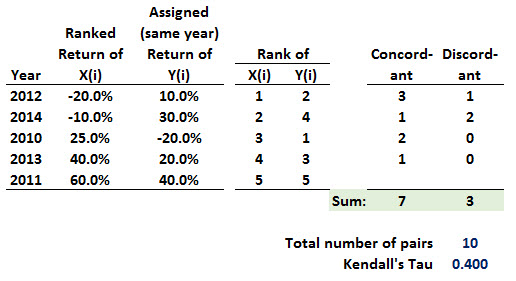
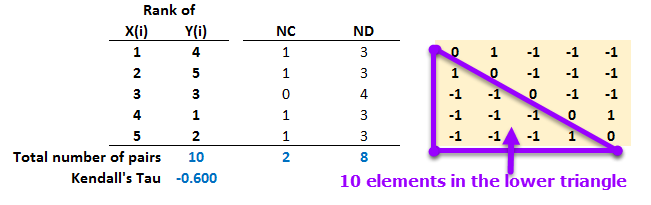
He writes "The pairs {( 1,4),( 3,3)}, {( 2,5),( 3,3)}, {( 3,3 ),( 4,1)}, and {( 3,3),( 5,2)} are neither concordant nor discordant" but I think that's because the formulas in 3.2.3. are mis-stated. {(1,4),( 3,3)} is discordant because the directionality of X(i) and Y(i) differ: 1 < 3 = X1 < X2 but 4 > 3 = Y2 > Y1. I borrowed Carol Alexander's spreadsheet (apparently, it is easy to get this wrong!) http://www.carolalexander.org/phpBB/viewtopic.php?f=4&t=159 which employs the elegant math of the wikipedia entry http://en.wikipedia.org/wiki/Concordant_pair. This helped me grok concordant/discordant (it's a first appearance in the FRM).
Take {(1,4),( 3,3)}. The Excel formula is =SIGN(X2 - X1)*SIGN(Y2 - Y1); if that = 1, it's concordant because they are ranking the same direction. If it's = -1, they are discordant. How can they be neither? If either X2 = X1 or Y2 = Y1, such that the product is zero.
In this way, I get eight discordant pairs (of pairs) and a Kendall's tau of -0.60.

My XLS is here https://www.dropbox.com/s/1f510upcpnp7ide/MR-9-kendalls-tau.xlsx?dl=0
He writes "The pairs {( 1,4),( 3,3)}, {( 2,5),( 3,3)}, {( 3,3 ),( 4,1)}, and {( 3,3),( 5,2)} are neither concordant nor discordant" but I think that's because the formulas in 3.2.3. are mis-stated. {(1,4),( 3,3)} is discordant because the directionality of X(i) and Y(i) differ: 1 < 3 = X1 < X2 but 4 > 3 = Y2 > Y1. I borrowed Carol Alexander's spreadsheet (apparently, it is easy to get this wrong!) http://www.carolalexander.org/phpBB/viewtopic.php?f=4&t=159 which employs the elegant math of the wikipedia entry http://en.wikipedia.org/wiki/Concordant_pair. This helped me grok concordant/discordant (it's a first appearance in the FRM).
Take {(1,4),( 3,3)}. The Excel formula is =SIGN(X2 - X1)*SIGN(Y2 - Y1); if that = 1, it's concordant because they are ranking the same direction. If it's = -1, they are discordant. How can they be neither? If either X2 = X1 or Y2 = Y1, such that the product is zero.
In this way, I get eight discordant pairs (of pairs) and a Kendall's tau of -0.60.
Last edited:

 ) mistakenly has: A pair is neither concordant nor discordant if x(t) = y(t) or x(t)* = y(t)*
) mistakenly has: A pair is neither concordant nor discordant if x(t) = y(t) or x(t)* = y(t)* Thanks!
Thanks!