P2.T8.401. Component and marginal value at risk (VaR) calculations

[David Harper CFA FRM]

Questions:

401.1. Consider the following three-asset portfolio and its correlation/covariance matrices:

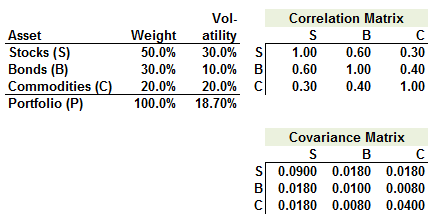
An asset's marginal risk (MRISK) is the asset's beta, with respect to the portfolio which includes the asset, multiplied by portfolio volatility; e.g., MRISK(S) = COV(S,P)/Variance(P)*Volatility(P) = COV(S, P)/Volatility(P). An asset's risk contribution (CRISK) is its marginal risk multiplied by it's weight; e.g., CRISK(S) = MRISK(S)*weight%(S). Risk contributions must sum to portfolio volatility (is their virtue!). Marginal VaR is MRISK scaled by the confidence level deviate; Component VaR is CRISK scaled by the deviate.

In the three-asset portfolio above, which is nearest to the risk contribution of the commodities (C) asset?

a. 2.075%
b. 3.740%
c. 4.938%
d. 5.010%


401.2. Consider the following three-asset portfolio (which assumes returns are multivariate normal):

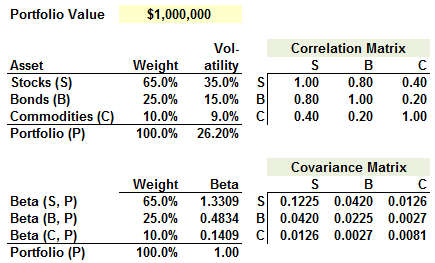
Which is nearest to the 95.0% component value at risk (VaR) of the bonds (B) position?

a. $17,800
b. $52,000
c. $93,500
d. $184,400


401.3. Consider the following three-asset portfolio:

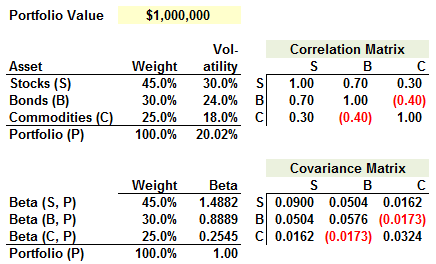
Each of the following statements is true EXCEPT which is false?

a. The 99.0% portfolio VaR is roughly $466,000
b. The stock (S) position has the highest 99.0% marginal VaR and the highest 99.0% component VaR, of the three positions
c. The commodities (C) position has a negative 99.0% marginal VaR
d. The incremental VaR of the commodity position is less than its component VaR

Answers:

• Here in forum

 

[Jackk90]

Hi @David Harper CFA FRM , in 401.2 I tried (probably wrongly) to obtain the component VaR for asset B obtaining the marginal VaR for B as difference between PTF VaR (S+B+C) - PTF VaR(S+C).

PTF Var with all the three asset is 1mln*26,2%*1,645=0,431mln

For VaR(S+C) I need the volatility of this PTF so I do sqrt(86,67%^2*35%^2 + 13,33%%^2*9%^2 + 2*0,4*86,67%*13,33%*35%+9%) and obtain 30,82%
(0,4 is the correlation S,C in the matrix, weights are rescaled from the weights of S,B,C)

VaR(S+C)=0,75mln*30,82%*1,645=0,380mln

Marginal VaR B = 0,431-0,380=0,051mln

Now given that Marginal Risk = Marginal VaR / 1,645 and Component VaR = Marginal Risk*weight*1,645...for the Component VaR B I just need to multiply for the weight 25% of B: 0,051*25%=0,0128mln

What am I missing?

Thank you

 

[gsarm1987]

Hi @David Harper CFA FRM , in 401.2 I tried (probably wrongly) to obtain the component VaR for asset B obtaining the marginal VaR for B as difference between PTF VaR (S+B+C) - PTF VaR(S+C).

PTF Var with all the three asset is 1mln*26,2%*1,645=0,431mln

For VaR(S+C) I need the volatility of this PTF so I do sqrt(86,67%^2*35%^2 + 13,33%%^2*9%^2 + 2*0,4*86,67%*13,33%*35%+9%) and obtain 30,82%
(0,4 is the correlation S,C in the matrix, weights are rescaled from the weights of S,B,C)

VaR(S+C)=0,75mln*30,82%*1,645=0,380mln

Marginal VaR B = 0,431-0,380=0,051mln

Now given that Marginal Risk = Marginal VaR / 1,645 and Component VaR = Marginal Risk*weight*1,645...for the Component VaR B I just need to multiply for the weight 25% of B: 0,051*25%=0,0128mln

What am I missing?

Thank you

Hi @David Harper CFA FRM , in 401.2 I tried (probably wrongly) to obtain the component VaR for asset B obtaining the marginal VaR for B as difference between PTF VaR (S+B+C) - PTF VaR(S+C).

PTF Var with all the three asset is 1mln*26,2%*1,645=0,431mln

For VaR(S+C) I need the volatility of this PTF so I do sqrt(86,67%^2*35%^2 + 13,33%%^2*9%^2 + 2*0,4*86,67%*13,33%*35%+9%) and obtain 30,82%
(0,4 is the correlation S,C in the matrix, weights are rescaled from the weights of S,B,C)

VaR(S+C)=0,75mln*30,82%*1,645=0,380mln

Marginal VaR B = 0,431-0,380=0,051mln

Now given that Marginal Risk = Marginal VaR / 1,645 and Component VaR = Marginal Risk*weight*1,645...for the Component VaR B I just need to multiply for the weight 25% of B: 0,051*25%=0,0128mln

What am I missing?

Thank you

Hello Jack, please allow me to answer: your calculation, "Marginal VaR B = 0,431-0,380=0,051mln" is actually the incremental VAR. Remember, Marginal is always for a small change (aka additional $ exposure) , where as incremental VAR is the one used for adding a new position.
Now for the formula to use for Component VAR, u need the Portfolio VAR, which you have calculated, next you need to multiply it with the Beta of B and weight of B, it should get you Component VAR of B
Formula for Component VAR is = Portfolio VAR X Beta of B X Weight of B
There is a variety of formulas to calculate this, refer to page 97 of formula sheet.
Let me know if that helps.


Marginal VAR = Change in VAR / Change in weight = alpha * change in stdv of portfolio / change in weight = alpha * Cov *(R, Rp)/stdevp

 

[Jackk90]

Hello Jack, please allow me to answer: your calculation, "Marginal VaR B = 0,431-0,380=0,051mln" is actually the incremental VAR. Remember, Marginal is always for a small change (aka additional $ exposure) , where as incremental VAR is the one used for adding a new position.
Now for the formula to use for Component VAR, u need the Portfolio VAR, which you have calculated, next you need to multiply it with the Beta of B and weight of B, it should get you Component VAR of B
Formula for Component VAR is = Portfolio VAR X Beta of B X Weight of B
There is a variety of formulas to calculate this, refer to page 97 of formula sheet.
Let me know if that helps.


Marginal VAR = Change in VAR / Change in weight = alpha * change in stdv of portfolio / change in weight = alpha * Cov *(R, Rp)/stdevp

Hi @gsarm1987, thank you very much for your answer, I absolutely confused Marginal VaR with Incremental VaR.