P2.T6.908. Credit exposure metrics (expected exposure and potential future exposure) (Gregory Ch.7)

[Nicole Seaman]

Learning objective: Describe and calculate the following metrics for credit exposure: expected mark-to-market, expected exposure, potential future exposure ....

Questions:

908.1. The probability distribution of the expected future value (EFV) of a position in a derivative contract is illustrated below:

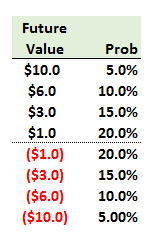
What is the expected exposure (EE) of this position?

a. Zero
b. 1.75
c. 3.50
d. 5.25


908.2. Suppose future value is defined by a normal distribution with mean, µ= $3.0 million, and standard deviation, σ = $5.0 million. Each of the following statements is true EXCEPT which is false?

a. The 99.0% potential future exposure (PFE) is about $14.63 million
b. The expected exposure (EE) must be greater than expected future value (EFV)
c. If volatility increases from σ = $5.0 to σ = $8.0 million, the EE will be unchanged
d. If volatility increases from σ = $5.0 to σ = $8.0 million, the 95% potential future exposure (PFE) will increase


908.3. Below is displayed the probability distribution of the future value (FV) for a position in a derivative contract. The distribution has a mean, µ = $3.0. Its standard deviation, σ = $12.56. Its skew is zero but it is not quite normal as its kurtosis is 2.95.

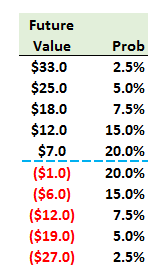
What is the 95.0% potential future exposure (PFE) of this position?

a. -19.00
b. +13.25
c. +25.00
d. +33.00

Answers here:

• In forum

 

[nikic]

For Q3, is it intuitive to us 2.33 as an approximation, where answer is 1.65 * 12.56 + 3.0 = 23.72. And then adjust this upwards as the standard deviation for the distribution with kurtosis of 2.95 should be slightly higher than that of the normal distribution?

 

[David Harper CFA FRM]

Hi @nikic I think that's clever (btw, I think you mean 2.33 for 99.0% approximation whereas your formula reflects a 95.0% VaR approximation and so uses 1.65): the distribution is nearly normal so you've approximated the 0.95 quantile with normal parameters. (on a really minor note, I'm thinking that if the above distribution has kurtosis < 3, then it has very slightly light tails such that you'd trim a bit down fro 23.72 rather than plus it up?). However, the above distribution is decidedly discrete (e.g., there are only ten outcomes, there are no asymptotic tails) such that the solution is dead-simple: we only need to locate the quantile directly on the table. While this question is trivial, there is a case when it's less trivial: if the question asked for the 97.5% VaR, then we can see that quantile lies exactly on the "border" between $33.0 and $25.0 and this is the infamous situation where there are at least three valid answers; e.g., $33.0, $25, or interpolation between the two. But my question 908.3 deliberately avoids that by locating the quantile "squarely" in the middle of its bin. Thanks,