P2.T6.710. Merton, survival time, and z-spread

[Nicole Seaman]

Concept: These on-line quiz questions are not specifically linked to learning objectives, but are instead based on recent sample questions. The difficulty level is a notch, or two notches, easier than bionicturtle.com's typical question such that the intended difficulty level is nearer to an actual exam question. As these represent "easier than our usual" practice questions, they are well-suited to online simulation.

Questions:

710.1. The risk management staff at an investment bank uses the Merton model to estimate the distance to default (DD) and expected default frequency (EDF) in evaluating default conditions for both potential and existing client firms. One such client currently has total assets valued at USD 20.0 billion, asset volatility, σ(A) of 28.0% per year, and debt with a face value of USD 12.0 billion. The expected return on the firm’s assets is 9.0% per year and the risk-free rate is 1.0% per year. The firm does not pay any dividends. The rating schedule at a 1-year horizon is shown in the table below: (inspired by GARP's 2017 P2 Question #3).

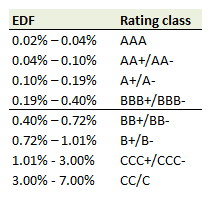
What is the suggested credit rating of the firm at a 1-year horizon using the provided rating schedule?

a. A+/A-
b. BBB+/BBB-
c. B+/B-
d. CCC+/CCC-


710.2. Below is plotted the cumulative survival time distribution under the assumption of a constant hazard rate.

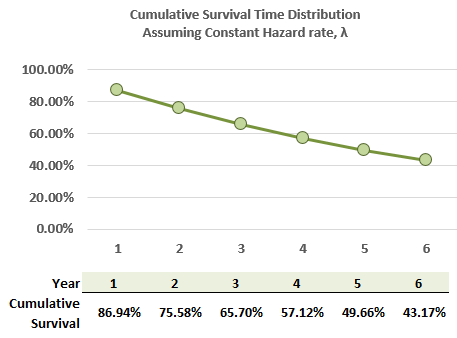
Each of the following statements about this plot is true EXCEPT which is false?

a. The hazard rate (aka, default intensity) is 14.0%
b. The five-year cumulative default probability is about 50.3%
c. The conditional default probability in year four is about 8.0%
d. The unconditional default probability in year three (i.e., joint probability of survival in first two years then default during third year) is about 9.9%


710.3. Consider a five-year bond that pays 7.0% semi-annual coupon. If we assume the upward-sloping risk-free zero rate curve shown below, where the zero rates are expressed with continuous compounding, then the bond's price is $103.57 and its implied yield 6.07% per annum with continuous compounding (which is equivalent to a yield of 6.16% with semi-annual compounding):

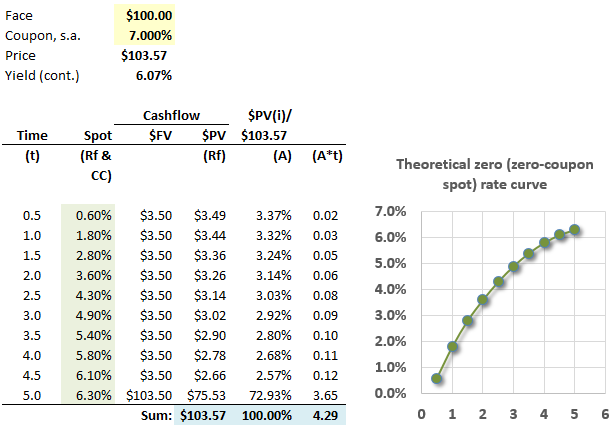
However, assume the bond actually trades at par (that is, it's current price is $100.00). If we recall that duration assumes a parallel shift in the rate curve (necessary given it is a single-factor model), which is nearest the bond's z-spread when this bond prices at par?

a. 82 basis point
b. 117 basis points
c. 153 basis points
d. 204 basis points

Answers here:

• In forum

 

[WhizzKidd]

Hi @David Harper CFA FRM

Out of interest. How would you price a credit risky bond? So given that a bond has a credit curve (CDS) (flat or otherwise), a recovery assumption and there exists a zero curve off which to price from.

What is interesting is that a z-spread is a flat rate added over a zero curve to get a model price of a bond to its market price. But when you use a credit curve, you cannot simply make the credit curve flat and equal to the z-spread, as you have to imply hazard rates from that curve for discounting and there is a recovery (R) which you don't use in normal bond valuation.

Just trying to understand the relation ship between what a z-spread is for an entity and why that is different to the CDS spread, from a valuation perspective. Because a z-spread is an implied rate and not really tradeable.

Curios as to how this works