Learning objectives: Define and calculate expected loss (EL). Define and calculate unexpected loss (UL). Estimate the variance of default probability assuming a binomial distribution. Calculate UL for a portfolio and the UL contribution of each asset.
Questions:
921.1. The following simplified credit rating transition matrix (aka, migration matrix) displays one-year conditional probabilities for only two credits (A and B). For example, the A-rated credit has an 80.0% probability of remaining A-rated at the end of the year, and a 20.0% probability of being downgraded to B-rated, but is not expected to default within one year. From year to year, migrations are independent; i.e., the matrix satisfies the Markov property.
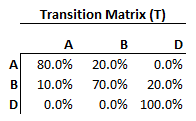
A bank has extended a three-year $15.0 million loan to a B-rated corporate borrower. The bank assumes the exposure at default (EAD) is the principal amount of $15.0 million and estimates a 40.0% recovery rate. If the relevant default probability is the three-year cumulative default probability, then what is the expected loss (EL)?
a. $1,800,000
b. $2,250,000
c. $3,978,000
d. $4,392,000
921.2. A credit portfolio contains an adjusted exposure of $30.0 million with a default probability of 4.0%. In regard to loss given default (LGD), the Portfolio Manager estimates an (LGD) of 40.0% with a standard deviation, σ(LGD), of 40.0%. What is the position's unexpected loss (UL)?
a. $2.250 million
b. $3.360 million
c. $5.490 million
d. $7.810 million
921.3. Consider a credit portfolio that contains the following two positions:
a. $14.2 and $5.8 million
b. $11.3 and $8.7 million
c. $9.5 and $10.5 million
d. $8.1 and $11.9 million
Answers here:
Questions:
921.1. The following simplified credit rating transition matrix (aka, migration matrix) displays one-year conditional probabilities for only two credits (A and B). For example, the A-rated credit has an 80.0% probability of remaining A-rated at the end of the year, and a 20.0% probability of being downgraded to B-rated, but is not expected to default within one year. From year to year, migrations are independent; i.e., the matrix satisfies the Markov property.

A bank has extended a three-year $15.0 million loan to a B-rated corporate borrower. The bank assumes the exposure at default (EAD) is the principal amount of $15.0 million and estimates a 40.0% recovery rate. If the relevant default probability is the three-year cumulative default probability, then what is the expected loss (EL)?
a. $1,800,000
b. $2,250,000
c. $3,978,000
d. $4,392,000
921.2. A credit portfolio contains an adjusted exposure of $30.0 million with a default probability of 4.0%. In regard to loss given default (LGD), the Portfolio Manager estimates an (LGD) of 40.0% with a standard deviation, σ(LGD), of 40.0%. What is the position's unexpected loss (UL)?
a. $2.250 million
b. $3.360 million
c. $5.490 million
d. $7.810 million
921.3. Consider a credit portfolio that contains the following two positions:
- $300.0 million exposure with default probability (PD) of 2.0%, loss given default (LGD) of 20.0% and σ(LGD) of 10.0%
- $100.0 million exposure with default probability (PD) of 6.0%, loss given default (LGD) of 60.0% and σ(LGD) of 30.0%
a. $14.2 and $5.8 million
b. $11.3 and $8.7 million
c. $9.5 and $10.5 million
d. $8.1 and $11.9 million
Answers here:
