Learning objectives: Identify and describe the characteristics and pay-off structure of the following exotic options: gap, forward start, compound, chooser, barrier, binary, lookback, shout, Asian, exchange, rainbow, and basket
Questions:
729.1 Consider an asset with a current price of $120.00 and volatility of 16.0% while the risk-free rate is 3.0%. A regular (aka, vanilla) but deeply out-of-the-money (OTM) one-year European put option on the stock with a strike price of $100.00 has a price of $0.740; i.e., p(S = $120.00, K = $100.00, σ = 0.160, Rf = 0.030, T = 1.0 year) = $0.740.
Now consider the modification of this regular put option into a gap put option with the addition of a trigger price, denoted K2. In this case, the price of the gap put option is given by p(S = $120.00, K1 = $100.00, K2 = trigger price, σ = 0.160, Rf = 0.030, T = 1.0 year). Each of the following statements about this gap option is true EXCEPT which is false?
a. If K1 = K2 = $100.00, then the gap option also has a price of $0.740
b. If the strike price, K1= $100.00 and the trigger price, K2 = $110.00, then the gap option has a negative price
c. If the strike price, K1 = $100.00 and the trigger price, K2 = $90.00, then the gap option price is greater than $0.740
d. Given a strike price, K1 = 100.00, among various trigger prices, the gap option has its highest price when the trigger, K2 = $100.00
729.2. The exhibit below shows the call option prices for various times to maturity, T = {three months, six months, nine months, 1.0 year, 1.25 years, and 1.5 years} for an at-the-money European call option while the stock and strike price are both $100.00, the stock's volatility (σ) is 30.0%, the risk-free rate is 7.0% and the stock pays a continuous dividend yield of 7.0%:
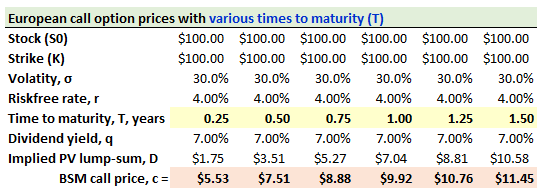
The stock price is $100.00 today. Consider a forward-start option that is a contract to buy, one year from today, a six-month to expiration at-the-money (ATM) call option; i.e., T1 = 1.0 year, T2 = 1.5 years. Which is nearest to the price of this forward-start option?
a. $7.00
b. $9.25
c. $10.68
d. $11.45
729.3. Consider a compound option that gives the holder the right to pay $1.90 in one year (T1) and purchase a call option with a strike price of $40.00 and one year to expiration; so this is a call-on-a-call with T1 = + 1.0 year and T2 = +2.0 years. The underlying stock price is currently $37.50. The stock's volatility is 30.0% and the riskfree rate is 4.0%. For convenience, the option prices of a one-year European call are shown below at stock prices according to $2.50 intervals:
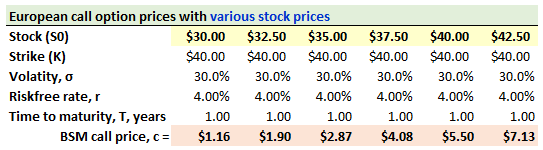
Under what condition(s) will this compound call-on-a-call option be exercised in one year?
a. This compound call will never be exercised
b. This compound call will be exercised if the stock price, S(1.0), is above $32.50
c. This compound call will be exercised if the underlying call has positive intrinsic value at time T1; i.e., if S(1.0) >= $40.00
d. The compound call will be exercised if the underlying call has a lower bound of $1.90 at time T1; i.e., if S(1.0) >= $40.33
Answers here:
Questions:
729.1 Consider an asset with a current price of $120.00 and volatility of 16.0% while the risk-free rate is 3.0%. A regular (aka, vanilla) but deeply out-of-the-money (OTM) one-year European put option on the stock with a strike price of $100.00 has a price of $0.740; i.e., p(S = $120.00, K = $100.00, σ = 0.160, Rf = 0.030, T = 1.0 year) = $0.740.
Now consider the modification of this regular put option into a gap put option with the addition of a trigger price, denoted K2. In this case, the price of the gap put option is given by p(S = $120.00, K1 = $100.00, K2 = trigger price, σ = 0.160, Rf = 0.030, T = 1.0 year). Each of the following statements about this gap option is true EXCEPT which is false?
a. If K1 = K2 = $100.00, then the gap option also has a price of $0.740
b. If the strike price, K1= $100.00 and the trigger price, K2 = $110.00, then the gap option has a negative price
c. If the strike price, K1 = $100.00 and the trigger price, K2 = $90.00, then the gap option price is greater than $0.740
d. Given a strike price, K1 = 100.00, among various trigger prices, the gap option has its highest price when the trigger, K2 = $100.00
729.2. The exhibit below shows the call option prices for various times to maturity, T = {three months, six months, nine months, 1.0 year, 1.25 years, and 1.5 years} for an at-the-money European call option while the stock and strike price are both $100.00, the stock's volatility (σ) is 30.0%, the risk-free rate is 7.0% and the stock pays a continuous dividend yield of 7.0%:

The stock price is $100.00 today. Consider a forward-start option that is a contract to buy, one year from today, a six-month to expiration at-the-money (ATM) call option; i.e., T1 = 1.0 year, T2 = 1.5 years. Which is nearest to the price of this forward-start option?
a. $7.00
b. $9.25
c. $10.68
d. $11.45
729.3. Consider a compound option that gives the holder the right to pay $1.90 in one year (T1) and purchase a call option with a strike price of $40.00 and one year to expiration; so this is a call-on-a-call with T1 = + 1.0 year and T2 = +2.0 years. The underlying stock price is currently $37.50. The stock's volatility is 30.0% and the riskfree rate is 4.0%. For convenience, the option prices of a one-year European call are shown below at stock prices according to $2.50 intervals:

Under what condition(s) will this compound call-on-a-call option be exercised in one year?
a. This compound call will never be exercised
b. This compound call will be exercised if the stock price, S(1.0), is above $32.50
c. This compound call will be exercised if the underlying call has positive intrinsic value at time T1; i.e., if S(1.0) >= $40.00
d. The compound call will be exercised if the underlying call has a lower bound of $1.90 at time T1; i.e., if S(1.0) >= $40.33
Answers here:
Last edited by a moderator:
