Learning objectives: Describe the four central moments of a statistical variable or distribution: mean, variance, skewness, and kurtosis. Interpret the skewness and kurtosis of a statistical distribution, and interpret the concepts of coskewness and cokurtosis. Describe and interpret the best linear unbiased estimator.
Questions:
712.1. Consider the following discrete probability distribution of asset returns:
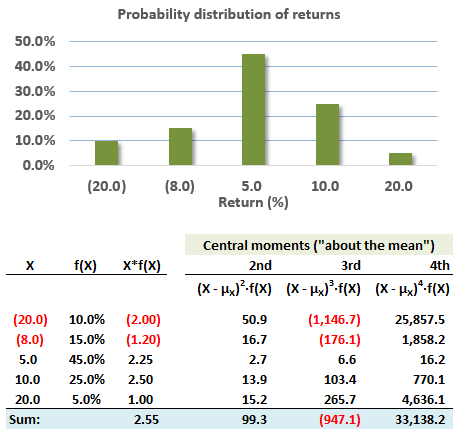
As shown, this asset's expected return is +2.55%. Which is nearest to this variable's skew; aka, standardized third central moment?
a. -2.25
b. -0.96
c. +0.33
d. +1.06
712.2. Consider the following discrete probability distribution of asset returns:
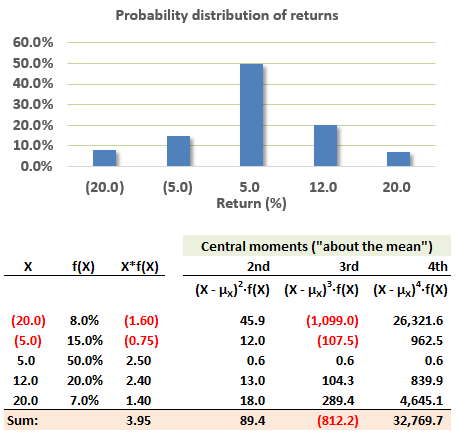
As shown, this asset's expected return is +3.95%. Which is nearest to this variable's kurtosis; aka, standardized fourth central moment?
a. -1.47
b. +2.81
c. +4.10
d. +7.50
712.3. Portfolio manager Peter manages a large portfolio with 100 component positions. He is interested in analyzing the non-trivial cross moments in the portfolio (trivial cross-moments are the position's coskew/cokurtosis with itself, which is simply the position's standard skew or kurtosis, so these are analogous to the diagonal of a covariance matrix which is mere variances. Peter already captures these trivial cross moments). Each of the following statements is true EXCEPT which is inaccurate?
a. Between any two (n = 2) positions in the portfolio, the number of non-trivial coskew moments between them is two
b. Between any two (n = 2) positions in the portfolio, the number of non-trivial cokurtosis moments between them is three
c. Given a sub-portfolio consisting of any two positions, lower coskew values (i.e., where positives are gains and negatives are losses) imply greater risk for the sub-portfolio
d. Although it is easy to estimate this portfolio's set of higher-order cross moments, standard skew and kurtosis are preferred because they are BLUE and the informational utility of coskew and cokurtosis is negligible
Answers here:
Questions:
712.1. Consider the following discrete probability distribution of asset returns:

As shown, this asset's expected return is +2.55%. Which is nearest to this variable's skew; aka, standardized third central moment?
a. -2.25
b. -0.96
c. +0.33
d. +1.06
712.2. Consider the following discrete probability distribution of asset returns:

As shown, this asset's expected return is +3.95%. Which is nearest to this variable's kurtosis; aka, standardized fourth central moment?
a. -1.47
b. +2.81
c. +4.10
d. +7.50
712.3. Portfolio manager Peter manages a large portfolio with 100 component positions. He is interested in analyzing the non-trivial cross moments in the portfolio (trivial cross-moments are the position's coskew/cokurtosis with itself, which is simply the position's standard skew or kurtosis, so these are analogous to the diagonal of a covariance matrix which is mere variances. Peter already captures these trivial cross moments). Each of the following statements is true EXCEPT which is inaccurate?
a. Between any two (n = 2) positions in the portfolio, the number of non-trivial coskew moments between them is two
b. Between any two (n = 2) positions in the portfolio, the number of non-trivial cokurtosis moments between them is three
c. Given a sub-portfolio consisting of any two positions, lower coskew values (i.e., where positives are gains and negatives are losses) imply greater risk for the sub-portfolio
d. Although it is easy to estimate this portfolio's set of higher-order cross moments, standard skew and kurtosis are preferred because they are BLUE and the informational utility of coskew and cokurtosis is negligible
Answers here:
Last edited by a moderator:
