Learning objectives: Calculate and interpret the covariance and correlation between two random variables. Calculate the mean and variance of sums of variables.
Questions:
711.1. The following probability matrix displays joint probabilities for an inflation outcome, I = {2, 3, or 4}, and an unemployment outcome, U = {5, 7 or 9}. Also shown are the expected values and variances for each random variable (e.g., the variance of the inflation random variable is 0.5690) and the expected value of their product, E(I*U) = 20.590.
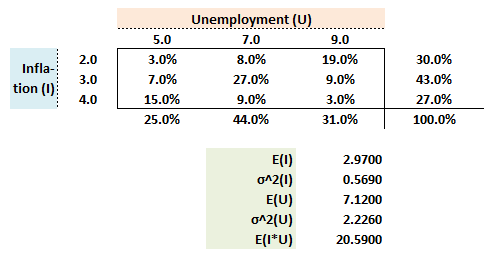
Which of the following is nearest to the correlation coefficient, ρ(I,U)?
a. -0.494
b. -0.137
c. Zero
d. +0.258
711.2. A discrete random variable can assume a value of {1, 2, 3, 4 or 5} with the following probabilities, where the sum of f(x)*X and and f(x)*X^2 is also shown:
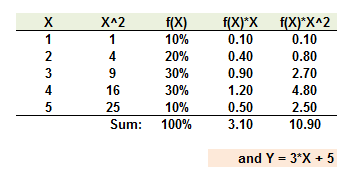
If Y = 3*X + 5, then what is the variance of Y, σ^2(Y)?
a. 1.29
b. 5.51
c. 11.61
d. 16.61
711.3. Consider a $100.00 position in Security A which has an expected return of 11.0% and volatility of 30.0%:
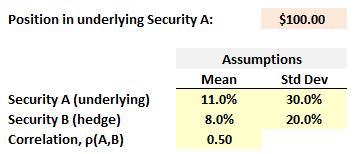
Security B has an expected return of 8.0%, volatility of 20.0% and its correlation to Security A, ρ(A,B) = +0.50. If we can only hedge this position by adding a position in Security B, then what trade will minimize the variance of the net portfolio? (note: This question applies Miller's Application: Portfolio Variance and Hedging in Chapter 3)
a. Zero (no additional position in Security B ensures the lowest portfolio volatility)
b. Long $33.0 in Security B
c. Short $75.0 in Security B
d. Short $167.0 in Security B
Answers here:
Questions:
711.1. The following probability matrix displays joint probabilities for an inflation outcome, I = {2, 3, or 4}, and an unemployment outcome, U = {5, 7 or 9}. Also shown are the expected values and variances for each random variable (e.g., the variance of the inflation random variable is 0.5690) and the expected value of their product, E(I*U) = 20.590.

Which of the following is nearest to the correlation coefficient, ρ(I,U)?
a. -0.494
b. -0.137
c. Zero
d. +0.258
711.2. A discrete random variable can assume a value of {1, 2, 3, 4 or 5} with the following probabilities, where the sum of f(x)*X and and f(x)*X^2 is also shown:

If Y = 3*X + 5, then what is the variance of Y, σ^2(Y)?
a. 1.29
b. 5.51
c. 11.61
d. 16.61
711.3. Consider a $100.00 position in Security A which has an expected return of 11.0% and volatility of 30.0%:

Security B has an expected return of 8.0%, volatility of 20.0% and its correlation to Security A, ρ(A,B) = +0.50. If we can only hedge this position by adding a position in Security B, then what trade will minimize the variance of the net portfolio? (note: This question applies Miller's Application: Portfolio Variance and Hedging in Chapter 3)
a. Zero (no additional position in Security B ensures the lowest portfolio volatility)
b. Long $33.0 in Security B
c. Short $75.0 in Security B
d. Short $167.0 in Security B
Answers here:
