Questions:
319.1. The current yield is 4.0% (with annual compounding) such that the price of a 12-year zero-coupon bond is $62.46, because 62.46 = 100/1.04^12. Assume the yield is normally distributed with basis point volatility of 85 basis points. For reference, here is a snippet of the standard normal CDF lookup table:
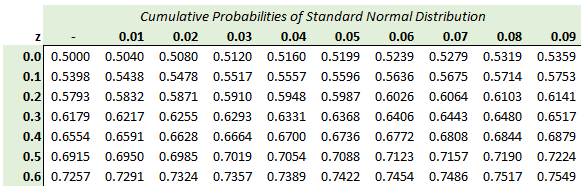
Which is nearest to the probability the bond price will fall below $60.00? (note: variation on FRM handbook discussion 2.3.5; single period assumed)
a. 29.5%
b. 34.1%
c. 48.0%
d. 55.3%
319.2. The following is a probability matrix for X = {1, 2, 3} and Y = {1, 2, 3}; i.e., the Joint Prob (X = 3, Y = 3) = 18.0%:
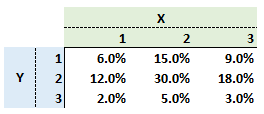
Each of the following is true EXCEPT which is false?
a. X and Y are independent
b. The covariance(X,Y) is non-zero
c. The probability Y = 3 conditional on X = 1 is 10.0%; i.e., Prob (Y = 3, X = 1) = 10.0%
d. The unconditional probability that X = 2 is 50.0%; i.e., Prob (X = 2) = 50.0%
319.3. A young credit agency has been rating bonds for the last five years. Peter analyzed their history. Among their coverage universe, 10% were rated "investment grade," 30% were rated "junk" and 60% were "Unrated." As such these are unconditional probabilities; i.e., Prob(I) = 10%, Prob(J) = 30%, and Prob (U) = 60%. He also computed conditional probabilities, as shown below. For example, the probability of an upgrade (within five years) conditional on an Investment rating is 8.0%; i.e., Prob (U | I) = 8%.
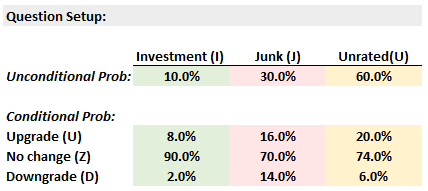
If a bond was downgraded, which is nearest to the probability it was rated Junk; i.e., what is Prob (J | D)?
a. 14.0%
b. 28.0%
c. 52.5%
d. 63.6%
Answers:
319.1. The current yield is 4.0% (with annual compounding) such that the price of a 12-year zero-coupon bond is $62.46, because 62.46 = 100/1.04^12. Assume the yield is normally distributed with basis point volatility of 85 basis points. For reference, here is a snippet of the standard normal CDF lookup table:

Which is nearest to the probability the bond price will fall below $60.00? (note: variation on FRM handbook discussion 2.3.5; single period assumed)
a. 29.5%
b. 34.1%
c. 48.0%
d. 55.3%
319.2. The following is a probability matrix for X = {1, 2, 3} and Y = {1, 2, 3}; i.e., the Joint Prob (X = 3, Y = 3) = 18.0%:

Each of the following is true EXCEPT which is false?
a. X and Y are independent
b. The covariance(X,Y) is non-zero
c. The probability Y = 3 conditional on X = 1 is 10.0%; i.e., Prob (Y = 3, X = 1) = 10.0%
d. The unconditional probability that X = 2 is 50.0%; i.e., Prob (X = 2) = 50.0%
319.3. A young credit agency has been rating bonds for the last five years. Peter analyzed their history. Among their coverage universe, 10% were rated "investment grade," 30% were rated "junk" and 60% were "Unrated." As such these are unconditional probabilities; i.e., Prob(I) = 10%, Prob(J) = 30%, and Prob (U) = 60%. He also computed conditional probabilities, as shown below. For example, the probability of an upgrade (within five years) conditional on an Investment rating is 8.0%; i.e., Prob (U | I) = 8%.

If a bond was downgraded, which is nearest to the probability it was rated Junk; i.e., what is Prob (J | D)?
a. 14.0%
b. 28.0%
c. 52.5%
d. 63.6%
Answers:
