Learning objectives: Explain how a probability matrix can be used to express a probability mass function. Compute the marginal and conditional distributions of a discrete bivariate random variable. Explain how the expectation of a function is computed for a bivariate discrete random variable.
Questions:
20.8.1. A stock (X1) has three possible returns: -5%, 0, or +5%. The analyst rating (X2) can be negative (denoted by X2= -1), neutral (X2 = 0), or positive (X2 = +1). The probability matrix is displayed below (inside the square). Six joint probabilities are given, but three are missing; for example, the joint probability of a negative analyst rating and a negative stock return, P(X1 = -5% ∩ X2 = -1) = 14.0%.
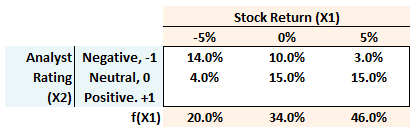
The bottom row (outside the square) displays the unconditional (aka, marginal) probabilities for the stock; for example, the unconditional Pr(X1 = -5%) = 20.0%. What is the unconditional (aka, marginal) probability that the analyst rating is positive, Pr(X2 = +1)?
a. 28.0%
b. 39.0%
c. 46.0%
d. 60.9%
20.8.2. The probability matrix below gives the joint probabilities for two variables, X1 and X2. The stock (X1) has three possible returns: -5%, 0, or +5%. The analyst rating (X2) can be negative (denoted by X2= -1), neutral (X2 = 0) or positive (X2 = +1). Also given are the marginal (aka, unconditional) probabilities for the stock (X1), as follows: Pr(X1 = -5%) = 20%, Pr(X1 = 0%) = 50% and Pr(X1 = +5%) = 30%.

What is the probability that the stock return is non-negative conditional on a positive analyst rating; i.e., what is conditional Pr[ (X1 = 0%) ∪ (X1 = +5%) | X2 = Positive]?
a. 45.00%
b. 66.67%
c. 75.00%
d. 93.75%
20.8.3. Below is a joint probability matrix for the variables X1 and X2.

What is the expected value of X1^X2?
a. 0.640
b. 3.671
c. 5.350
d. 6.500
Answers here:
Questions:
20.8.1. A stock (X1) has three possible returns: -5%, 0, or +5%. The analyst rating (X2) can be negative (denoted by X2= -1), neutral (X2 = 0), or positive (X2 = +1). The probability matrix is displayed below (inside the square). Six joint probabilities are given, but three are missing; for example, the joint probability of a negative analyst rating and a negative stock return, P(X1 = -5% ∩ X2 = -1) = 14.0%.
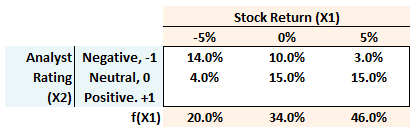
The bottom row (outside the square) displays the unconditional (aka, marginal) probabilities for the stock; for example, the unconditional Pr(X1 = -5%) = 20.0%. What is the unconditional (aka, marginal) probability that the analyst rating is positive, Pr(X2 = +1)?
a. 28.0%
b. 39.0%
c. 46.0%
d. 60.9%
20.8.2. The probability matrix below gives the joint probabilities for two variables, X1 and X2. The stock (X1) has three possible returns: -5%, 0, or +5%. The analyst rating (X2) can be negative (denoted by X2= -1), neutral (X2 = 0) or positive (X2 = +1). Also given are the marginal (aka, unconditional) probabilities for the stock (X1), as follows: Pr(X1 = -5%) = 20%, Pr(X1 = 0%) = 50% and Pr(X1 = +5%) = 30%.

What is the probability that the stock return is non-negative conditional on a positive analyst rating; i.e., what is conditional Pr[ (X1 = 0%) ∪ (X1 = +5%) | X2 = Positive]?
a. 45.00%
b. 66.67%
c. 75.00%
d. 93.75%
20.8.3. Below is a joint probability matrix for the variables X1 and X2.

What is the expected value of X1^X2?
a. 0.640
b. 3.671
c. 5.350
d. 6.500
Answers here:
