Learning objectives: Describe an event and an event space. Describe independent events and mutually exclusive events. Explain the difference between independent events and conditionally independent events.
Questions:
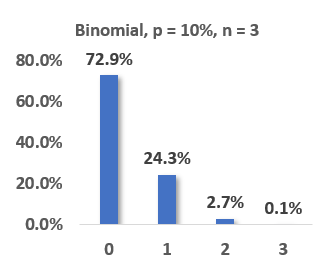
20.1.1. A specialized credit portfolio contains only three loans but they are very risky, as each has a single-period default probability of 10.0%. They are independent (therefore, we have the i.i.d. condition). You know enough probability to determine (for example) that, at the end of a single period, the probability that all three loans default is 0.1% and the probability that all three loans survive is 72.9%. However, at the end of the period, the portfolio manager gives you a piece of additional information when she tells you that "AT LEAST two of the bonds have defaulted." What is the (conditional) probability that the other (third) bond also defaulted?
a. 0.09%
b. 0.10%
c. 3.57%
d. 10.0%
20.1.2. Yesterday a web page hosted by Acme received tens of thousands of page views but some were views by malicious bots. Acme utilizes two software applications to detect these malicious "bot-views." It uploads the same data file from yesterday to both applications. The first application detects 200 bot-views and the second application detects 300 bot-views. Among these, only 40 bot-views were detected by both applications. All bot-views are equally likely to be located, but clearly both applications only identify a minority of the bot-views (otherwise there would be a much higher number of identified bot-views common to both applications). Further, the identification of a bot-view by one application is independent of its identification by the other application. How many malicious bot-views did the web page experience on this day?
a. 300
b. 460
c. 540
d. 1,500
20.1.3. Albert and Betty share an office where each month they attempt to predict the best-performing industry within their respective sectors. Albert's sector is Financials and Betty's sector is Information Technology. Each contains several industries. Without any help, the probability that Albert predicts the best-performing industry (within Financials) is 12.0%, and the probability that Betty predicts the best-performing industry (within I.T.) is 15.0%. Put another way, their unconditional success probabilities are, respectively, P(A) = 12.0% and P(B) = 15.0%. Without any help, the probability that they both simultaneously predict their best industry is 1.80%; that is, the joint Pr(A ∩ B) = 1.80%. Their firm also subscribes to software with artificial intelligence and the software boosts their predictive abilities. In fact, when using the software to help them, their respective success probabilities double. Specifically, P(A | S) = 24.0% and P(B | S) = 30.0%; for example, the probability that Betty picks the best-performing industry conditional on her utilization of the software jumps to 30.0%. When they both use the software, their joint probability of success is 15.0%. In regard to the observed dependencies, which of the following statements is accurate?
a. Independent and conditionally independent
b. Independent but conditionally dependent
c. Dependent but conditionally independent
d. Dependent and conditionally dependent
Answers here:
Questions:
20.1.1. A specialized credit portfolio contains only three loans but they are very risky, as each has a single-period default probability of 10.0%. They are independent (therefore, we have the i.i.d. condition). You know enough probability to determine (for example) that, at the end of a single period, the probability that all three loans default is 0.1% and the probability that all three loans survive is 72.9%. However, at the end of the period, the portfolio manager gives you a piece of additional information when she tells you that "AT LEAST two of the bonds have defaulted." What is the (conditional) probability that the other (third) bond also defaulted?
a. 0.09%
b. 0.10%
c. 3.57%
d. 10.0%
20.1.2. Yesterday a web page hosted by Acme received tens of thousands of page views but some were views by malicious bots. Acme utilizes two software applications to detect these malicious "bot-views." It uploads the same data file from yesterday to both applications. The first application detects 200 bot-views and the second application detects 300 bot-views. Among these, only 40 bot-views were detected by both applications. All bot-views are equally likely to be located, but clearly both applications only identify a minority of the bot-views (otherwise there would be a much higher number of identified bot-views common to both applications). Further, the identification of a bot-view by one application is independent of its identification by the other application. How many malicious bot-views did the web page experience on this day?
a. 300
b. 460
c. 540
d. 1,500
20.1.3. Albert and Betty share an office where each month they attempt to predict the best-performing industry within their respective sectors. Albert's sector is Financials and Betty's sector is Information Technology. Each contains several industries. Without any help, the probability that Albert predicts the best-performing industry (within Financials) is 12.0%, and the probability that Betty predicts the best-performing industry (within I.T.) is 15.0%. Put another way, their unconditional success probabilities are, respectively, P(A) = 12.0% and P(B) = 15.0%. Without any help, the probability that they both simultaneously predict their best industry is 1.80%; that is, the joint Pr(A ∩ B) = 1.80%. Their firm also subscribes to software with artificial intelligence and the software boosts their predictive abilities. In fact, when using the software to help them, their respective success probabilities double. Specifically, P(A | S) = 24.0% and P(B | S) = 30.0%; for example, the probability that Betty picks the best-performing industry conditional on her utilization of the software jumps to 30.0%. When they both use the software, their joint probability of success is 15.0%. In regard to the observed dependencies, which of the following statements is accurate?
a. Independent and conditionally independent
b. Independent but conditionally dependent
c. Dependent but conditionally independent
d. Dependent and conditionally dependent
Answers here:
Last edited: