P1.T1.401. Arbitrage pricing theory (APT) for well-diversified portfolios
AIMs: Describe the Law of One Price and assess whether an arbitrage situation exists using a multi-factor model. Construct the Security Market Line for a well-diversified portfolio using a single-factor model. Explain how to construct a portfolio to hedge exposure to multiple factors. Describe the Arbitrage Pricing Theory (APT) and the Fama-French three-factor model, and explain the underlying assumptions of each.
Questions:
401.1. Consider the following three well-diversified portfolios that exist in a single-factor economy:
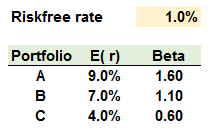
Is there an arbitrage opportunity?
a. No, all three well-diversified portfolios plot on the security market line
b. Yes, an arbitrage includes buying portfolio (A) and selling a combination of (B) and (C)
c. Yes, an arbitrage includes buying portfolio (B) and selling a combination of (A) and (C)
d. Yes, an arbitrage includes buying portfolio (C) and selling a combination of (A) and (B)
401.2. Consider the following multi-factor (APT) model of security returns for a particular stock, along with actual-versus-expected rates of change in the three macro factors:
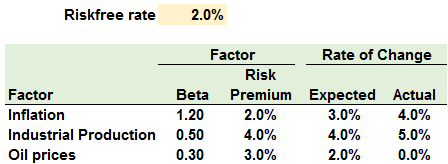
If we include the "surprises" in the macro factors, what is the expected rate of return for the stock?
a. 5.30%
b. 7.30%
c. 8.40%
d. 9.90%
401.3. Assume two portfolios, (A) and (B), are each well-diversified and the economy has only one factor. The expected return of portfolio (A) is 8.0% and its beta is 1.30. The expected return of portfolio (B) is 6.0% and its beta is 0.90. What is the implied risk-free rate?
a. 1.50%
b. 2.25%
c. 3.00%
d. 5.75%
Answers here:
AIMs: Describe the Law of One Price and assess whether an arbitrage situation exists using a multi-factor model. Construct the Security Market Line for a well-diversified portfolio using a single-factor model. Explain how to construct a portfolio to hedge exposure to multiple factors. Describe the Arbitrage Pricing Theory (APT) and the Fama-French three-factor model, and explain the underlying assumptions of each.
Questions:
401.1. Consider the following three well-diversified portfolios that exist in a single-factor economy:

Is there an arbitrage opportunity?
a. No, all three well-diversified portfolios plot on the security market line
b. Yes, an arbitrage includes buying portfolio (A) and selling a combination of (B) and (C)
c. Yes, an arbitrage includes buying portfolio (B) and selling a combination of (A) and (C)
d. Yes, an arbitrage includes buying portfolio (C) and selling a combination of (A) and (B)
401.2. Consider the following multi-factor (APT) model of security returns for a particular stock, along with actual-versus-expected rates of change in the three macro factors:

If we include the "surprises" in the macro factors, what is the expected rate of return for the stock?
a. 5.30%
b. 7.30%
c. 8.40%
d. 9.90%
401.3. Assume two portfolios, (A) and (B), are each well-diversified and the economy has only one factor. The expected return of portfolio (A) is 8.0% and its beta is 1.30. The expected return of portfolio (B) is 6.0% and its beta is 0.90. What is the implied risk-free rate?
a. 1.50%
b. 2.25%
c. 3.00%
d. 5.75%
Answers here:
Last edited by a moderator:
