Kavita.bhangdia
Active Member
Hi David,
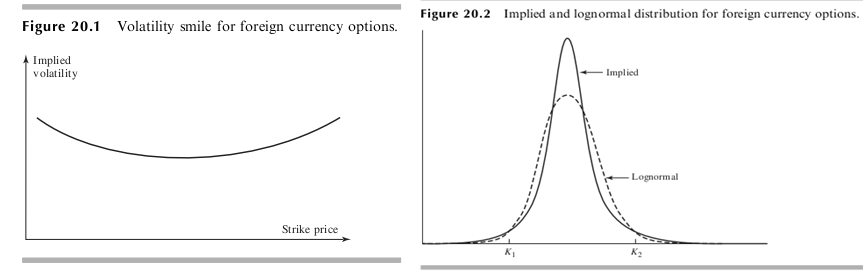
How do we find the shape on the implied vol curve based on the shape of distribution of underlying..
Thanks
Kavita
How do we find the shape on the implied vol curve based on the shape of distribution of underlying..
Thanks
Kavita
Last edited: