My issue is prompted by the provided answer and explanagion for Q16 in Mock Exam A. Because the floating rate used to generate the first year payment is not given, the methodology discounts the future cash flows from years 2 and years 3 (including the notional "principle") back to year 1 using continuous compounding. Fine. This give a fixed leg value at year one (before exchange of payments for that year) of the $408.25 as stated. However, the corresponding floating leg value is given as the notional $400. However, this is true only if annual compounding is used - the floating rate value at the time of the second year payment is 400 * 1.o4. If this is discounted back to the first year with a discount factor of the reciprocal of 1.o4, using annual compounding, the value of the floating leg at year 1 is indeed $400. However, since continuous compounding was used for the fixed leg, shouldn't continuous compounding be used for the floating leg as well (as it is in Ch 7 of Hull viz (L+K* x exp(-r*t*)) so that the floating valuation should in fact be $416 *exp(-.04*1) = $399.68 and the value to the bank is -8.56 not -8.25.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Mixing continuous and annual compounding in interest rate swap valuation
- Thread starter neveo
- Start date
Hi @neveo
Astute observation. But the next floating coupon is not $16.00 = 4.00% * $400. Rather it will be $16.324 = 4.0811%*400, as 4.08% is the annual equivalent of 4.00% continuous; exp(0.04)-1=4.0811%. There is indeed a mixing (is your astute observation!): the 6.0% coupon is an annual rate, yet the 4.00% and 4.80% are continuous rates. I copied the underlying XLS below, which shows the value under both approaches, "as two bonds" and "as FRAs." Please note the three orange rows under FRA where:
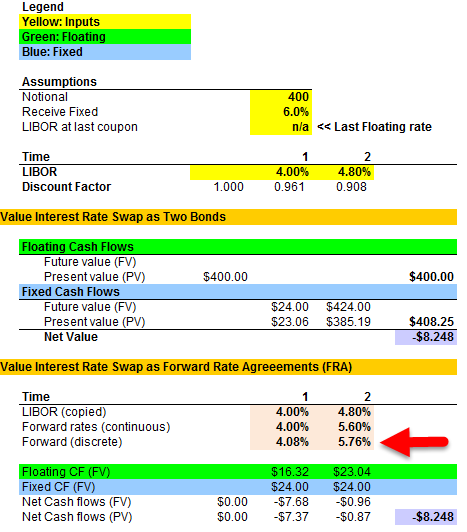
Astute observation. But the next floating coupon is not $16.00 = 4.00% * $400. Rather it will be $16.324 = 4.0811%*400, as 4.08% is the annual equivalent of 4.00% continuous; exp(0.04)-1=4.0811%. There is indeed a mixing (is your astute observation!): the 6.0% coupon is an annual rate, yet the 4.00% and 4.80% are continuous rates. I copied the underlying XLS below, which shows the value under both approaches, "as two bonds" and "as FRAs." Please note the three orange rows under FRA where:
- First the LIBOR spote (continuous), then
- The implied forwards (continuous) translated
- implied forwards (annual)

Yes,
Yes, otherwise the whole concept of the swap rate being a par rate falls apart! A floater is just a rolled forward set of of par bonds. If the coupon is set by the same curve as the discount curve, it should discount to par.Hi @neveo
Astute observation. But the next floating coupon is not $16.00 = 4.00% * $400. Rather it will be $16.324 = 4.0811%*400, as 4.08% is the annual equivalent of 4.00% continuous; exp(0.04)-1=4.0811%. There is indeed a mixing (is your astute observation!): the 6.0% coupon is an annual rate, yet the 4.00% and 4.80% are continuous rates. I copied the underlying XLS below, which shows the value under both approaches, "as two bonds" and "as FRAs." Please note the three orange rows under FRA where:
Pricing the floater at par ($400) is tautological. It, by definition, assumes the coupon rate which (in this case) is annual is equal to the discount rate. If the discount rate were 4.0% with annual compounding, then it prices to par if the annual coupon is 4.0% because 416/1.04 = 400. But the discount rate is 4.0% with continuous, such that pricing to par requires (and implies) an annual coupon of 4.0811%. Please note this is consistent with Hull's steps in Example 7.3 where the mixing of compound frequencies requires the translation of implied continuous forward to discrete (s.a. in that example) rates. I hope that explains, thanks,
- First the LIBOR spote (continuous), then
- The implied forwards (continuous) translated
- implied forwards (annual)

Re "Yes, otherwise the whole concept of the swap rate being a par rate falls apart! A floater is just a rolled forward set of of par bonds" Exactly, it could not be said with better precision 

Hi, This question reminds of an old question. We have 2 ways to calculate the value of a swap, the bond method and the forward rate agreement method. Which one do you consider a faster way to solve for value in the exam ? I think its the bond method. Having said that, are there any exceptional questions where the bond method cannot be used ?
Hi @NNath I tend to agree with you. My longstanding habit is to value the swap per the forward rate method, simply because this mimics the actual mechanics so i find it slightly more intuitive (i.e., forward rates anticipate the expected future net settlements, and those net cash flows are discounted). However, you might like to look at https://forum.bionicturtle.com/threads/l1-t3-176-currency-swap-valuation.4587/
... where recently somebody pointed out that it's much quicker to use the bond method.
... I personally cannot recall an instance where the forward rate approach was required. Similar to how our XLS reconciles the two methods, under any set of input assumptions to my knowledge, I *think* the bond approach should always be available. Thanks,
... where recently somebody pointed out that it's much quicker to use the bond method.
... I personally cannot recall an instance where the forward rate approach was required. Similar to how our XLS reconciles the two methods, under any set of input assumptions to my knowledge, I *think* the bond approach should always be available. Thanks,
Hi David,
I am very new to the Forum and have got a few naive questions.
Re the swap valuation in the Learning spreadsheet T3.12.7_Swaps(worksheet SWAP(IRS)). My confusion lies with the way the FRA method of valuation works.
When the CFs for the floating is calculated the semi-annual forward rates are calculated from the continuous ones and then the CFs derived by multiplying with 0.5 as it is semiannual.
Yellow: Inputs
Green: Floating
Blue: Fixed
Assumptions
Notional 100
Receive Fixed 8.0%
LIBOR at last coupon 10.2% << 1st floating rate in SEMI-ANNUAL
Time 0.25 0.75 1.25
LIBOR 10.0% 10.5% 11.0%
Discount Factor(Continuous) 0.975 0.924 0.872
Floating Cash Flows
Future value (FV) $105.10
Present value (PV) $102.51 $102.51
Fixed Cash Flows
Future value (FV) $4.00 $4.00 $104.00
Present value (PV) $3.90 $3.70 $90.64 $98.24
Net Value $4.27
Time 0.25 0.75 1.25
LIBOR (copied) 10.00% 10.50% 11.00%
Forward rates (continuous) 10.75% 11.75%
Forward (semi-annual) 10.20% 11.04% 12.10%
Floating CF (FV) $5.10 $5.52 $6.05
Fixed CF (FV) $4.00 $4.00 $4.00
Net Cash flows (FV) $1.10 $1.52 $2.05
Net Cash flows (PV) $1.07 $1.41 $1.79 $4.27
I am very new to the Forum and have got a few naive questions.
Re the swap valuation in the Learning spreadsheet T3.12.7_Swaps(worksheet SWAP(IRS)). My confusion lies with the way the FRA method of valuation works.
When the CFs for the floating is calculated the semi-annual forward rates are calculated from the continuous ones and then the CFs derived by multiplying with 0.5 as it is semiannual.
- What I didn't understand is why the discounting of both legs happening using continuous discounting and not semi-annual discounting? There is no consistency in the way the CF and the discounting are calculated. How will I know in the exam whether to use continuous discounting or semi-annual as in the below case? Is there a certain rule that FRM follows for these kind of questions, say, the discounting will always be continuous and the CFs to be calculated as per periodic compounding???
- The calculations are time consuming for the purpose of the exam. Can we store the formula in the calculator? I have HP 17BII+ calculator.
- Is there an easy way to calculate the ACT/ACT calculations using the calculator or is it done manually?
- The Forward semi-annual calculated in Swap(IRS) worksheet is different from the "Swap (IRS, but semi-annual)" worksheet, Is it because in the "Swap(IRS)" worksheet we are considering the LIBOR as continuous compounding rates where as in the "Swap (IRS, but semi-annual)" worksheet we are considering as semi-annual compounding rates?
- If that is the case as in q4 how will we come to know in the exam what exactly to consider the LIBOR rates? Continuous or periodic compounding???
Yellow: Inputs
Green: Floating
Blue: Fixed
Assumptions
Notional 100
Receive Fixed 8.0%
LIBOR at last coupon 10.2% << 1st floating rate in SEMI-ANNUAL
Time 0.25 0.75 1.25
LIBOR 10.0% 10.5% 11.0%
Discount Factor(Continuous) 0.975 0.924 0.872
Floating Cash Flows
Future value (FV) $105.10
Present value (PV) $102.51 $102.51
Fixed Cash Flows
Future value (FV) $4.00 $4.00 $104.00
Present value (PV) $3.90 $3.70 $90.64 $98.24
Net Value $4.27
Time 0.25 0.75 1.25
LIBOR (copied) 10.00% 10.50% 11.00%
Forward rates (continuous) 10.75% 11.75%
Forward (semi-annual) 10.20% 11.04% 12.10%
Floating CF (FV) $5.10 $5.52 $6.05
Fixed CF (FV) $4.00 $4.00 $4.00
Net Cash flows (FV) $1.10 $1.52 $2.05
Net Cash flows (PV) $1.07 $1.41 $1.79 $4.27
Last edited:
Hi @INDRAJIT
- The swap valuation implements the assigned John Hull's (Chapter 7 Swaps) approach. The Swap(IRS) implements the approach of his example 7.2 (i.e., swap "coupon" cash flows expressed with semi-annual compounding, yet discount rates with continuous). I added Swap(IRS, but semi-annual) merely to illustrate that both approaches (valuation of swap as two bonds or FRAs) produces two equal results. In Hull, the reason for continuous discounting is simply that continuous is his default compound frequency; probably due to its elegant time-additive properties. In regard to coupon cash flows, it's more natural: rhetorical question, what would be the meaning of (eg) a swap that pays 6% per annum every six months with continuous compounding? It is sort of hard to grasp that. Instead, just like a bond, the compound frequency matches the coupon frequency, such that (eg.) if the swap pays 6.0% per annum with semi-annual compounding, then it's a very natural idea to compute each six month payment as (notional)*6%/2. Re: Is there a certain FRM rule? No, not really. As discussed many many times in this forum, the GARP's current approach is to specify on the exam.
- You could certainly store portions in the calculator (I personally do that; e.g., the value of each leg), but I am not aware of a way to fruitfully generalize the entire swap calculation into the calculator. But no matter: the IRS swap valuation is assigned not really because you will need to replicate the same entire (tedious) calculation, the exam is not "cruel" like that frankly (caveat: there are simple variation is the test body, but they tend not to require compound frequency translation). I would prefer to think of the application of the swap, for exam purposes as: 1. As a concept, which might be tested it only its simplest variation; and 2. As a bundle of components, or pieces, which might be tested in isolation; e.g., the mere translation of a rater.
- I don't think day count conventions are utilized in this swap exercise? In any case, the TI BA II+ does have day count convention in its bond worksheet, but I have never used the bond worksheet in the TI (it simply is not necessary).
- Yes, exactly. As above, I added the semi-annual worksheet, in response to a forum question, simply to demonstrate that we are rarely locked into a compound frequency choice. The member got different answers under the bond-versus-FRM approaches, so I just wanted to show that it does not matter which approach we use, if we are careful about consistency in the compound frequency.
- GARP will specify. I have repeatedly requested an overall "default" choice, to keep things simpler; it would be helpful if candidates could prepare generally with a single approach. But, currently, that is not the approach. I hope that helps!
Hi @David Harper CFA FRM CIPM I am going through the example on page 101 Hull Chap 7. I dont get how the forward rates are calculated. Appreciate if you can show/explain it to me. Thanks heaps!
Similar threads
- Replies
- 0
- Views
- 238
- Replies
- 2
- Views
- 561
- Replies
- 0
- Views
- 1K
- Replies
- 0
- Views
- 254
