Key rates

[ChristofferLoov]

Hi David,

I’m trying to wrap my head around key rates and therefore have a few questions. I tried searching the forum but couldn’t find the answer.

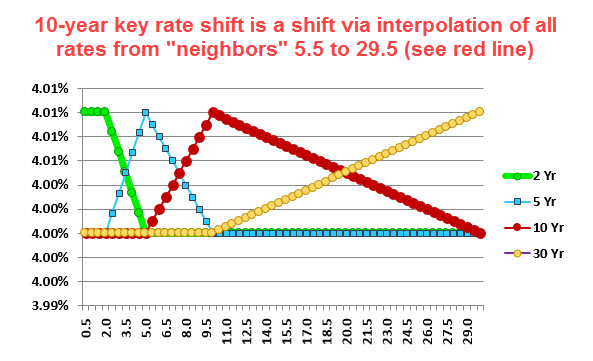
1. In Tuckmans example all securities seems to have the same maturity as a key rate, but one point of key rates were to keep them as few as possible for hedging purposes. What happens if I have a zero coupon bond with a maturity of 14 years but my closest key rates are for 10 and 30 years? Do I use linear interpolation to distribute the cash flows to those key rates?
2. Tuckman says that we select the most liquid government securities to calculate the key rates. However in his example he calculates different key rate 01 and durations for each bond in the portfolio. If we select government securities as a benchmark, shouldn’t the key rate 01 and duration for all bonds in the portfolio be the same? Or is it the case that since we have 4 key rates in the example, the shortest maturity will have 4 KR01, the next will have 3 KR01 and so on?
3. If that is not the case how does that impact the number of simultaneous equations we have to solve to hedge the exposure?

 

[David Harper CFA FRM]

HI @ChristofferLoov Okay sure, although at a certain point, my experience is that it's best to try and scrutinize the spreadsheet implementation of key rates if only because its hard to just describe in words the mechanics. But here is my perspective:

1. Yes, almost correct (it's inaccurate to say "distribute the cash flows to those key rates?" as we don't alter the cash flows of the instrument/hedge portfolio). When we use DV01, we re-price the bond by shocking (changing) the yield-to-maturity by one basis point; regardless of the shape of the spot rate term structure, this is tantamount to shifting the interest rate term structure in parallel by one basis point. We can think of the key rate technique as an alternative to this parallel shift: instead of shifting the whole curve, we "break it up" into the number of segments per our number of key rates; e.g., Tuckman uses four key rates at 2-, 5-, 10- and 30- years such that his technique "breaks up" the shift into four segments. Regardless of the instrument, but including your 14-year maturity bond example, the technique replaces (under single-factor duration) its sensitivity to a parallel shift with its sensitivity to shifts in each of the four key rates. But importantly, the shift of the key rate is the shift of all rates extending from its lower-maturity neighbor to its higher-maturity neighbor via linear interpolation. For example, any bond's key rate '01, KR01, with respect to the 10-year rate will be its price change (given its unaltered cash flows) due to a shift in the key rate and all of the rates extending to its neighboring key rate. See my screenshot below. Shifting/shocking the 10-year key rate is not a shock of a single 10-year spot rate, rather it is a shift of all of the par rates (because that's the interest rate he selected) from 5 years to 30 years via linear interpolation. The linear interpolation determines the rate shift for all the neighboring rates; e.g., 5.5 year par rate, 6.0 year par rate, 6.5 par rate ... 20.0 year par rate, 29.5 par rate. So, Tuckman's example segments the term structure into four segments or regions, if you will: {0 to 2.0}, {2.0 to 5.0}, {5.0 to 10.0} and {10.0 to 30.0}. The 10-year KR01, aka KR01[10], is the price change given shifting all of the rates from 5.5 years to 29.5 years via linear interpolation. Linear interpolation ensures that, if we shock all key rates, we end up shocking the entire term structure.
2. Tuckman suggests it is helpful to select key rates (e.g., 2-year, 5-year) that can be easily hedged with liquid securities such as U.S. Treasury. However, each bond has its own sensitivity (per the calculation) to a shift in a key rate (which, again, is really a shift of all rates that extend to neighboring rates, albeit declining via the linear interpolation). Just like various bonds have various reactions to a single-factor parallel shift in yield-to-maturity. But this is not greatly problematic because the KR01s, like DV01s (as illustrated by Tuckmans example) can be added together.
3. It is true that the number of simultaneous equations can get large, however, at a certain point it is not necessary to solve the entire hedging portfolio to zero at all key rates. This is illustrated by Tuckman's alternative hedge where he only neutralizes the two key rates where the exposure is largest. Whereas his "strict solution" neutralizes all four key rates perfectly (i.e., summing exposure and hedge to zero), his alternative hedge is imperfect and settles for some non-zero outcomes in favor of a simpler solution.

 

[ChristofferLoov]

Thanks David, this helps a lot!