Branislav
Member
Dear David,
Thanks a lot for video lectures they are much inspiring Still I was little bit confused with all these different names duration, modified duration, Macauly duration,.. etc...I will shortly examine mine view of this and kindly ask you to comment ( but without laughing )
)
According to mine understanding we are methodologically speaking about one risk measure all the time, called duration - how long on average shall i wait as bond holder to receive cash payments, or in terms on formula as you explained ( formula 1):
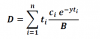
From this formula we see that that when we say on average, we are referring to time weighted average, so as a result for 3 year maturity bond I will obtain let's say 2.63 - so this is time based measure ( for zero coupon bond it is equal to 3- no cash flows till the very same end, if you can wait that much
If you agree with me on this definition than this is the same thing as Macaulay duration, there is nothing new coming with this new name introduced beside of course great honor and memory on Frederick Macauly who introduced this concept.
So we are still on duration and keep playing further. What if we do the first derivative by yield, just to check what is bond's sensitivity on yield change..
Delta (B)=dB/dY*Delta(y) ( formula 2 ) and dB/dY is "similar" to the right side of the formula 1, just with the minus in front , and we need to "remove" B from the denominator, or put it another way: dB/dY=-B*D and using formula 2 we obtain ( let us call it " yield/price sensy formula"):
For me this was kind of "magic"..somehow mine year based measure D becomes interest ( yiedl) sensitivity measure!
But basically we are still talking about duration from the beginning of the text, just with this simple "math" transformation we saw that it is also connected to the bonds price sensitivity to yield change
We play further ...we assumed above continuous compounding, if we go to the annual compounding, then, bond price is little bit different summation:
...we assumed above continuous compounding, if we go to the annual compounding, then, bond price is little bit different summation:
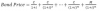
( note just the yield y is replaced with i) and duration and its first derivative are little bit different, so their relationship from " yield/price sensy formula"is now transforme to :
Thanks a lot in advance
Thanks a lot for video lectures they are much inspiring Still I was little bit confused with all these different names duration, modified duration, Macauly duration,.. etc...I will shortly examine mine view of this and kindly ask you to comment ( but without laughing
 )
)According to mine understanding we are methodologically speaking about one risk measure all the time, called duration - how long on average shall i wait as bond holder to receive cash payments, or in terms on formula as you explained ( formula 1):
From this formula we see that that when we say on average, we are referring to time weighted average, so as a result for 3 year maturity bond I will obtain let's say 2.63 - so this is time based measure ( for zero coupon bond it is equal to 3- no cash flows till the very same end, if you can wait that much

If you agree with me on this definition than this is the same thing as Macaulay duration, there is nothing new coming with this new name introduced beside of course great honor and memory on Frederick Macauly who introduced this concept.
So we are still on duration and keep playing further. What if we do the first derivative by yield, just to check what is bond's sensitivity on yield change..
Delta (B)=dB/dY*Delta(y) ( formula 2 ) and dB/dY is "similar" to the right side of the formula 1, just with the minus in front , and we need to "remove" B from the denominator, or put it another way: dB/dY=-B*D and using formula 2 we obtain ( let us call it " yield/price sensy formula"):
Delta (B)=-B*D*Delta(y)
For me this was kind of "magic"..somehow mine year based measure D becomes interest ( yiedl) sensitivity measure!
But basically we are still talking about duration from the beginning of the text, just with this simple "math" transformation we saw that it is also connected to the bonds price sensitivity to yield change
We play further
 ...we assumed above continuous compounding, if we go to the annual compounding, then, bond price is little bit different summation:
...we assumed above continuous compounding, if we go to the annual compounding, then, bond price is little bit different summation:( note just the yield y is replaced with i) and duration and its first derivative are little bit different, so their relationship from " yield/price sensy formula"is now transforme to :
Delta (B)=-B*D*Delta(y)/(1+y)
and we introduce new "name" again, "Modified duration" as:
D*=D/(1+y), which transforms previous equation to:
Delta (B)=-B*(D*)*Delta(y)
so again D* is duration from the beginning of the text, just for yearly compounding case, "used" in this formula to express sensitivity of bonds price on yield change.and we introduce new "name" again, "Modified duration" as:
D*=D/(1+y), which transforms previous equation to:
Delta (B)=-B*(D*)*Delta(y)
Thanks a lot in advance
