GARCH equations

[Mohamed.FRM]

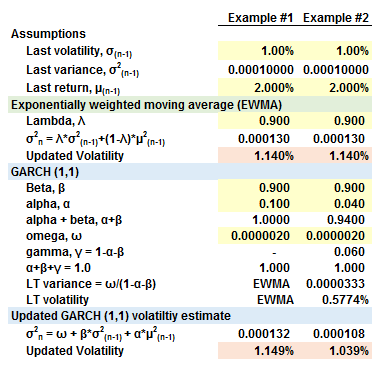
1- for FRM exam purpose, what is the required information to be memorized regarding GARCH equation?
2- Could you please provide Detailed explanation/answer for the following question?

Consider the following four GARCH equations:

Equation 1: σ2n = 0.83 + 0.05μ2n-1 + 0.93σ2n-1
Equation 2: σ2n = 0.06 + 0.04μ2n-1 + 0.95σ2n-1
Equation 3: σ2n = 0.60 + 0.10μ2n-1 + 0.94σ2n-1
Equation 4: σ2n = 0.03 + 0.03μ2n-1 + 0.93σ2n-1

Which of the following statements regarding these equations is (are) CORRECT?

I.Equation 1 is a stationary model.

II.Equation 2 shows no mean reversion

III.Volatility will revert to a long run mean level faster with Equation 1 than it will for Equation 4.

IV.Volatility will revert to a long run mean level faster with Equation 3 than it will for Equation 2.

• A)III only.
  B)II and III only.
  C)II and IV only.
  D)I only.

 

[David Harper CFA FRM]

Hi @mohamedcia

taking 2) first, it's an interesting question. Each of the question is a variation on the same GARCH concept of persistence, which is given by alpha (weight on recent return^2) plus beta (weight on recent variance). So:

I. GARCH is (covariance) stationary when it's persistence < 1.0. Equations 1, 2 and 4 are stationary but 3 is not b/c its a+b = .10+.94 = 1.04 > 1.0. So (I) looks TRUE.
II. For our non-technical purposes, stationary should imply mean reversion b/c (a+b) < 1.0 implies a positive, non-zero weight (typically called 'gamma') on the long-run, unconditional variance. Therefore, the same 1, 2, and 4 which are stationary similarly exhibit mean reversion. So, this (II) looks FALSE.
III. faster mean reversion is relative but would be indicated by LOWER persistence of (a+b), or conversely, faster mean reversion would be indicated by higher gamma. Where a+b+gamma = 1.0, necessarily. So, in order of fastest mean reversion (most to least), we'd have: #4 with gamma = 0.04, #1 with gamma = 0.02, and #2 with gamma of 0.02 (the #3 with a non-stationary negative gamma such that we'd probably not use it). Ergo, this (III) is FALSE
IV. As above, FALSE.

fwiw, the omegas (0.83, 0.06, 0.60, and 0.03) are not realistic: they are too high. For the FRM exam, a key formula is long run (unconditional) variance = omega/gamma = omega /(1-a-b) where omega = LR variance*gamma. In #1, for example, gamma must be 0.02, which is realistic, but that implies a LR variance of 41.5 which is awkwardly high. I hope that helps!

 

[m123mikmik]

@David Harper CFA FRM CIPM - Following up on @mohamedcia 's questions. Do you feel it's necessary to memorize the GARCH, EWMA, ARCH and / or the Forecasting Volatility Forward K days equation? I certainly realize there are some similarities but it would be one less thing to worry about if I don't have to memorize them...

 

[David Harper CFA FRM]

History suggests the FRM tends to favor the application of GARCH/EWMA; i.e., most popular is to give the model with params and ask for updated volatility estimate. This sort of common question does not really require a "memorization" so much as familiarity.

I probably would memorize: GARCH's long run (unconditional) variance = omega/(1-alpha-beta), where omega is the first constant in GARCH, and understand why that works, because it's a popular way to query GARCH.

I would memorize EWMA as it's testable and relatively easy.

I'm "on the fence" with respect to forecasting forward the future GARCH volatility: it's not an obvious formula so it's effort to memorize, yet it's testability is low, but possible. If I had to *guess*, I'd say you don't need to memorize the forward formula given the conceptual (non-quantitiative) AIM: "Explain how GARCH models perform in volatility forecasting" ... I think GARP is getting more realistic on some of these concepts, testing the idea more than a rote memorization. I hope that helps!

 

[m123mikmik]

@David Harper CFA FRM CIPM - That's perfect! Thanks so much!

 

[Priyanka_Chandak23]

Could someone please provide me with the formula of covariance calculation for GARCH and EWMA model when estimating the changed correlation?
There are two assets A and B with change in their prices and previous day's volatities and correlation. I have calculated the changed volatities but somehow am not being able to recall the formula for covariance in both the models so cannot compute the changed correlation. Please help!

Thanks.

 

[ShaktiRathore]

EWMA: Cov(n)=lambda*Cov(n-1) + (1-lambda)*x(n-1)*y(n-1)
where Cov(n-1) is the covariance estimate for day n-1 and x(n-1)*y(n-1) is the cross product of the returns for x and y on day n-1.
for GARCH: Cov(n)=omega+beta*Cov(n-1) + alpha*x(n-1)*y(n-1) where omega is the LT average Covariance component,we just introduced this component ito the EWMA model to get to the GARCH.
thanks

 

[Suphi]

@David Harper CFA FRM

Hi,

We have an issue that is about calculating VaR. Our model is currently calculating VaR by using 2 types of methods EWMA and GARCH under the Monte Carlo Similation and the Historical Similation.

Our dataset contains 252 days (1 year) but, comparing these two models (EWMA and GARCH) we are using day to day approache which included the days of february.(20 days). At the end we have 4 types of outputs which comprise Historical outputs by using EWMA, Historical outputs by using GARCH, Monte Carlo outputs by using EWMA, Monte Carlo outputs by using GARCH. In these set of materials are showing us there are no differences between GARCH outputs and EWMA outputs. However, we were doing a literature review. In these kind of researches show us that should be a different between GARCH outputs and EWMA outputs. In these conditions, what do you think that can arise the problem that creates the same result to us?

Secondly, we have considered that there are no differences between the outputs by comparing different value of Lambda Value. For instance, we put 0.99 for lambda value and then 0.94 as well. When we compared the different values of Lambda we didn’t have changes for EWMA and GARCH outputs as well.

Actually we came across in the literatuly that there shouldn’t be any lambda value for GARCH models. But our model does. What is your opinion about this complication?

We have request to answer these questions which are highly essential for us.

Thank you for your interesting.

 

[David Harper CFA FRM]

Hi @Suphi If your format is Excel, feel free to share and I can take a quick look and tell you what I think. EMWA's lambda, λ, weights the exponential decline of squared returns and is analogous to GARCH(1,1)'s beta, β. If GARCH has any weight on mean reversion, the results should differ. GARCH reduces to EWMA if the weight assigned to long-run (aka, unconditional) variance, in which case that would explain identical results. Changing EWMA's lambda (like changing GARCH's beta) should alter the result. These are not complicated models generally, so it's sometimes more efficient to just look at the model rather than use words. If you post, I will give it try when I get a chance but we prioritize FRM exam needs especially during the month before the exam. Good luck!

 

[David Harper CFA FRM]

@Suphi this might help, here is a sheet from our learning workbook ("R25-P1-T4-Allen-VaR-volatility-v5"): https://www.dropbox.com/s/ba6i7idi09ykqqr/0426-garch-versus-ewma.xlsx?dl=0
This is a comparison between EWMA and GARCH(1,1). In the first column (Example #1) I simply assigned to GARCH weights β=0.90 and α=0.10 such that α+β=1.0 and forces gamma (γ, the weight to the LR variance) to be zero, and you can see in that special case the updated volatility is the same as EWMA with λ=0.90. Example #2 switches GARCH α down to 0.040 so that γ has non-zero weighting and then the difference between GARCH and EWMA is introduced. Hopefully this XLS is helpful. Thanks!