FRM Fun Question 20: Option value with infinite term

[David Harper CFA FRM]

P1 or P2.

@[email protected] posted another provocative question here. She observes:

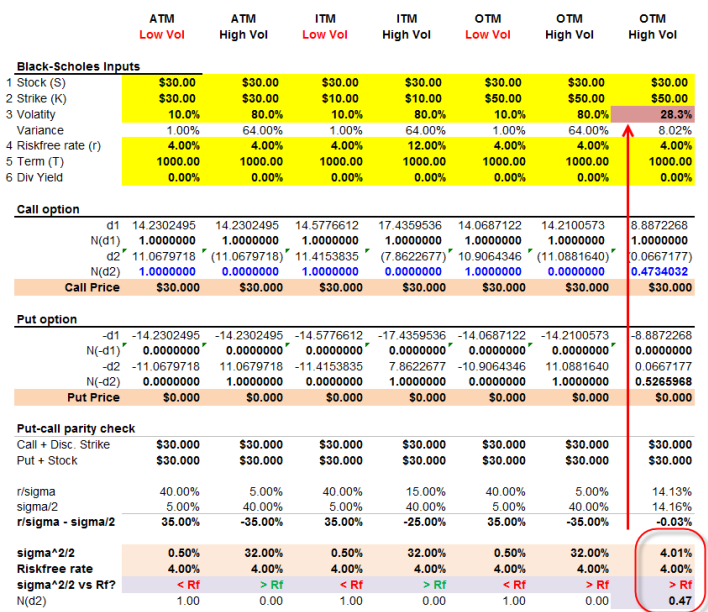
According to Hull as the time to expiration increases, options become more valuable. [But] when I check this with the Black Scholes formula: Put = K*exp(-rT)*N(-d2)-S*N(-d1), it appears that N(-d2) tends to 1; N(-d1) tends to zero, and exp(-rT) tends to zero ... I conclude that the put price tends to zero.

Questions:

1. Is she mathematically correct and, if so, what is a (relatively) simple interpretation?
2. Does a call option have a similar limit/asymptote (as term extends) at zero? If so/not, what is a similar interpretation?

 

[ShaktiRathore]

1.
c(0)= S(0)*N(d1)- K*exp(-rT)*N(d2)
d1= ln(S(0)/X)+T*(r+.5sigma^2)/σ*√T
d2= ln(S(0)/X)+T*(r-.5sigma^2)/σ*√T

Assuming that S0>X;
as T -> +∞ => d1->+∞ =>N(d1)->1
case i) S(T)>X stock price at time T as T approaches +∞
=>
N(d2) which is probability of S(T)>X is 1=> N(d2)=1
c(0)= S(0)*1- K*exp(-rT)*1
c(0)= S(0)*1- K*0*1 (as exp(-rT)->0 as T -> +∞ )
c(0)= S(0)
case ii) S(T)<X stock price at time T as T approaches +∞
N(d2) which is probability of S(T)>X is 0=> N(d2)=0
c(0)= S(0)
so in the case of call option the call price approaches stock price when time to maturity approaches infinity. This is due to the positive effect of N(d1) which increases with T.
2.
p(0) = K*exp(-rT)*N(-d2)-S(0)*N(-d1)
Assuming that S0>X;
as T -> +∞ => d1->+∞ =>N(d1)->1=>N(-d1)=1-N(d1)=0
case i) S(T)>X stock price at time T as T approaches +∞
=>
N(-d2) which is probability of S(T)<X is 0=> N(-d2)=0
p(0) = K*exp(-rT)*0-S(0)*0
p(0)= 0
case ii) S(T)<X stock price at time T as T approaches +∞
N(-d2) which is probability of S(T)<X is 0=> N(-d2)=1
p(0)= K*exp(-rT)*N(-d2)-S(0)*N(-d1)
p(0)= K*exp(-rT) which is present value of exercise price receives at maturity T but as T approaches +∞ the present value gets smaller and smaller until it becomes so small that it reaches zero. As N(-d2) which is the probability of S(T)<X increases as T increases the value of put increases so its not wrong to argue that value of put option increases with maturity in the sense that the positive effect of N(-d2) outweighs the negative effect of exp(-rT). So when we comprehend this with exp(-rT)*N(-d2) together the net effect of increase in T is that the value of the put option increases as time to maturity increases.The value of N(-d1) also decreases from 1 to 0 so that it has positive effect on put price as the T increases.

thanks

 

[David Harper CFA FRM]

Hi Shakti,

Thanks, this is a GREAT answer. It agrees with my simulation because you have attached the condition of future S(T), not current S(0), versus current strike (X). And that agrees with mathless summary of the mathematical dynamic ("d2 changes sign from positive to negative as relationship of r changes from less than to more than sigma^2/2").

Since d2 = [ln(S/K) + (r-sigma^2)*T]/[sigma*SQRT(T)], as T --> +∞ , LN(S/K) has no impact (~ 0), so we have d2 = [(r-sigma^2)*T]/[sigma*SQRT(T)] = (r-sigma^2)*SQRT(T)/sigma, and the direction hinges on (r-sigma^2); i.e., if sigma^2>r, then volatility overcomes the riskless drift and, in the limit, d2 is negative (same as your S(t) < X; I suppose distribution-wise this is a lognormal median that is tending toward zero in the limit, fascinating!).

fwiw, here is a snapshot of my XLS simulation that comports with your formulation above (i.e., when T = 1,000 years, if sigma^2/2 << Rf, then N(d2) ~= 1 and if sigma^2/2 >> Rf, then N(d2) ~= 01.0. Similarly, under any long term (T), see last column, N(d2) can be restored to values like ~0.5 if we solve for sigma^2/2 ~= Rf)

The XLS file is here, snapshot: