F- Statistic Formula Variations

[gargi.adhikari]

Hi,
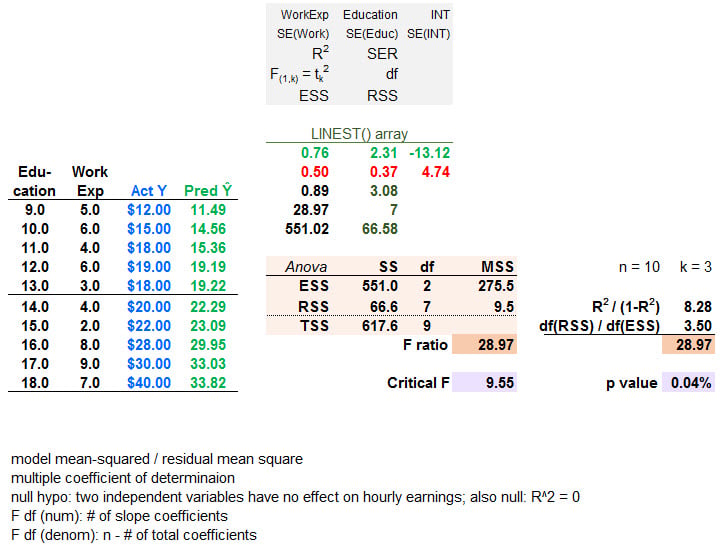
@David Harper CFA FRM had indicated in a thread that -" The general form of the F-statistic is F[numerator df, denominator df] = (ESS/df)/(RSS/df) "

F -Statistic is also expressed as = {Sum Of Squares BETWEEN / df-BETWEEN } / { Sum Of Squares WITHIN / df-WITHIN } => This expression of the F-Statistic I conceptually and intuitively understand.

However, there are some other Variations for the F -Statistic Formula
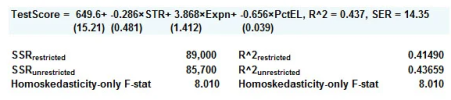
F -Statistic = { ( SSR-Restricted - SSR-UNRestricted ) / No of Restrictions } / (SSR-UNRestricted ) /(N-k-1) which again I understand the conceptually and intuitively.

Also,
F -Statistic = { (R-UNRestricted ^2 - R-Restricted ^ 2 ) /q } / ( 1- R-UNRestricted ^2 ) / (N-k-1)


How does ( SSR-Restricted - SSR-UNRestricted ) translate to (R-UNRestricted ^2 - R-Restricted ^ 2 ) given that in general, R^2 = { 1 - SSR/ (SSR + SSExplained)

 

[David Harper CFA FRM]

Hi @gargi.adhikari After @Nicole Seaman posts the F-ratio video to our YouTube section, I will edit the summary below for greater clarity. For the moment, because I don't have much extra bandwidth, I am going to "collect" the first rough draft; we have a useful tag = https://forum.bionicturtle.com/tags/f-statistic/ which contains the key prior conversations. Below are three references.

In brief summary:

• In my opinion, the most relevant (especially for exam purposes) regression F-statistic is explained in my YouTube video below (Reference #3 below). This most relevant is the most basic and is called by S&W the "overall" regression F-statistic because it tests the joint (null) hypothesis that all slope coefficients are zero. And this is typically how we first encounter it: this null posits that jointly β1 = 0 ∩ β2 = 0 ∩ β3 = 0 ∩ ... ∩ βn = 0 for a "total of q restrictions" so the alternative is that "one or more of the restrictions does not hold."
  • This overall regression, as I explain in Reference #1 below, is a special case of S&W's homoskedastic F-stat given by 7.14:
    F = [(R^2 - R^2 restricted)/q] / [(1-R^2)/(n - k unrestricted - 1), but it is the special case where q = k = the number of regressors in the unrestricted regression), such that: F = [(R^2 - 0)/k] / [(1-R^2)/(n - k - 1)] = [(R^2/k)]/[(1-R^2)/(n-k-1)].
  • As my video illustrates (and its XLS demonstrates), this "overall" regression F-statistic is equivalently given by F=(ESS/df)/(RSS/df). That is, the overall F = [(R^2/k)]/[(1-R^2)/(n-k-1)] = (ESS/df)/(RSS/df), where k = ESS(df) = number of slope coefficients (excluding intercept), and as usual RSS(df) = n - k - 1.
• The "more sophisticated" F test, discussed in my Reference #2 below, involves a joint test not of all the slope coefficients (as above) but rather a joint test of some subset of the coefficients; e.g.., my example below refers to S&W's example regression that has three independent variables (PctEL, STR, and Expn) but only two restrictions (i.e., "the joint null is that both STR and Expn are equal to zero."). This is not an "overall" F test; this is called the homoskedasticity-only F-statistic and it utilizes the latter variants that you have listed. That's just all I have time for now, this is a rough draft meant to pull the conversation together into a coherent whole; later I will refine for a better post, and insertion into the study note. Thanks,

Reference #1 at https://forum.bionicturtle.com/threads/f-statistic.7676/ i.e.,

Hi Brian,
It's a smart question

The reason I didn't include F = (ESS/df)/(RSS/df) is that I don't think S&W show it. Inexplicably, as that was the more familiar (and intuitive) formula before S&W replaced previous, better econometric readings (I think S&W on F-stat is *weak* and confusing)).

F = (ESS/df)/(RSS/df) is the F stat for the so-called "overall" regression F-stat; i.e., the test of the joint null that all regressors (independent variables) are equal to zero. This is the basic F-stat. We want to note that this is a special case of a restricted regression: the test of joint null that all independents = 0 is equivalent to restricting all of the regression coefficients (i.e., q = number of independent variables). Again, the (common) overall regression F-stat is a special case of a restricted regression where restrictions (q) is set equal to number of independents (which is equal to ESS df).

So this overall F-stat is a special case of S&W's homoskedastic F-stat given by 7.14:
F = [(R^2 - R^2 restricted)/q] / [(1-R^2)/(n - k unrestricted - 1), but the special case where q = k = the number of regressors in the unrestricted regression), such that:
F = [(R^2 - 0)/k] / [(1-R^2)/(n - k - 1)] = [(R^2/k)]/[(1-R^2)/(n-k-1)].

So, as far as I am concerned, there is one general F-stat and the difference is the number of restrictions. I'm not aware that the FRM has ever gone beyond the "overall" regression F-stat. (given this, the t^2 should only be equivalent when the unrestricted regression happens to have two independent variables: in which case, the overall F-stat is a test of the joint null that two regressors are zero). I hope that explains.

Reference #2 at https://forum.bionicturtle.com/threads/stock-watson-chap-7.13787/post-58778 i.e.,

Hi @FlorenceCC The F-statistic applies to the test of a joint hypothesis that several regression coefficients are equal to zero, according to the null. See our exhibit below, which replicates S&W's example. This is an regression with three independent variables such that TestScr = b0 + b1*PctEl + b2*Expn + b3*STR. The "overall regression" F-statistic is typically generated by the software; in my Excel below, =LINEST produces this overall regression F-stat = 107.455. But it can also be found with (ESS/df)/(RSS/df) = (66,410/3)/(87,500/416) = 107.455. It is potentially confusing because you might logically say that "this typical F-statistic is testing the joint null hypothesis that all three regressands are equal to zero, which is the special case of three restrictions," but S&W are calling this an unrestricted regression. That is, if we are restricting all of the coefficients (aka, imposing restrictions on all of the coefficients), it is the "unrestricted" regression! (which makes some sense actually)

Then, separately, in the exhibit below, there are homoskedastic-only F-stats = 8.010, calculated per F-stat as function of SSR (like your equation above) and R^2, restricted versus unrestricted. This is following S&W's example. These 8.01 are not a joint test of all three coefficients, but rather a joint test with only two (2) restrictions, q = 2: the joint null is that both STR and Expn are equal to zero. The F-stat of 8.01 uses as inputs either the unrestricted SSR (85,700) or unrestricted R^2 (0.437) which are produced by the overall regression. I hope that helps clarify!

Reference #3 is my recent YouTube video: The F ratio is a test of overall significance in a multivariate regression (FRM T2-20) which uses the regression below to illustrate

That video ("The F ratio is a test of overall significance in a multivariate regression (FRM T2-20)" is located here:

 

[yLam4028]

does the two formulas converge assuming the multiple regression has k independent variables and our null hypotheses is ALL k slope coefficients are zero ( so q=k) ?

 

[gsarm1987]

@yLam4028 if one independent variable, t^2 = F, but when more non zero independent variables then this won't hold. Formula for F-test = Regressed sum of squares / Sum of squared Errors

 

[yLam4028]

thank you ! I mean if restriction = # of independent variables, are they the same:

(ESS/df)/(RSS/df)
and
{ (R-UNRestricted ^2 - R-Restricted ^ 2 ) /q } / ( 1- R-UNRestricted ^2 ) / (N-k-1)

 

[David Harper CFA FRM]

@yLam4028 Your question doesn't make a lot of sense to me (and could be time-consuming to decipher) because if your premise is true (i.e., if restriction = # of independent variables) then why are we applying the second formula with "restricted R^2"?

I do not want to get us bogged down in this, but maybe this will be helpful. Consider my Reference #2 (at https://forum.bionicturtle.com/threads/stock-watson-chap-7.13787/post-58778) where the F-stat is 8.010 because 2 out of 3 are restricted. Now just take the case of an "unrestricted" regression with all three slope coefficients:

As I wrote there, the F-stat is 107.455 per (new emphasis mine)

Hi @FlorenceCC The F-statistic applies to the test of a joint hypothesis that several regression coefficients are equal to zero, according to the null. See our exhibit below, which replicates S&W's example. This is an regression with three independent variables such that TestScr = b0 + b1*PctEl + b2*Expn + b3*STR. The "overall regression" F-statistic is typically generated by the software; in my Excel below, =LINEST produces this overall regression F-stat = 107.455. But it can also be found with (ESS/df)/(RSS/df) = (66,410/3)/(87,500/416) = 107.455. It is potentially confusing because you might logically say that "this typical F-statistic is testing the joint null hypothesis that all three regressands are equal to zero, which is the special case of three restrictions," but S&W are calling this an unrestricted regression. That is, if we are restricting all of the coefficients (aka, imposing restrictions on all of the coefficients), it is the "unrestricted" regression! (which makes some sense actually)

Now notice we can also find it with: (see that table for these values):

[R^2/(k-1)] / [(1-R^2)/(n-k)] = [0.437 / (4-1)] / [(1-0.437)/(420-4)] = (0.145530781 / 0.001354345) = 107.4547069.
... where this R^2 is the "unrestricted R^2"

which is to be expected because it's a special case (per above) ...

F = [(R^2 - R^2 restricted)/q] / [(1-R^2)/(n - k unrestricted - 1), but the special case where q = k = the number of regressors in the unrestricted regression), such that:
F = [(R^2 - 0)/k] / [(1-R^2)/(n - k - 1)] = [(R^2/k)]/[(1-R^2)/(n-k-1)].

... so I guess the answer to your question is "yes" but to me that is the same thing as saying that the F ratio in an "unrestricted" regression (i.e., where the joint null is ALL slope coefficients equal to zero) can be retrieved in either way:

overall F = [(R^2/k)]/[(1-R^2)/(n-k-1)] = (ESS/df)/(RSS/df)

 

[yLam4028]

thank you David for your clarification! it is much clearer to me now. Sorry for asking this weird question.
So as you said the F test using EES/RES is a special case of the restricted & unrestricted version. They are equivalent and they will return the same value in that special case.

I am asking the question because I want to validate whether

"if all variables are being tested, ( SSR-Restricted - SSR-UNRestricted ) yield EES"

now I know it is true and SSR-Restricted with all variables tested should equal sum of square of ( Actual Y- Mean of Y) so that their difference would be the sum of square of explained residuals ( Predicted y - Mean of Y ).

thank you once again.

one last question for restricted F test - say we force all independent variables to have a coefficient of 0 except one.
For that one independent variable, do we model the intercept and coefficient again ? or we take the existing values from the unrestricted model directly?

 

[David Harper CFA FRM]

Hi @yLam4028

If you examine the example at https://forum.bionicturtle.com/threads/stock-watson-chap-7.13787/post-58778 ...
It refers to a regression with three independent variables: TestScore = Intercept + PctEL*X1 + Expn*X2 + STR*X3
The unrestricted regression (where q = 3) generates a highly significant F-stat if 107.5 per

This is an regression with three independent variables such that TestScr = b0 + b1*PctEl + b2*Expn + b3*STR. The "overall regression" F-statistic is typically generated by the software; in my Excel below, =LINEST produces this overall regression F-stat = 107.455. But it can also be found with (ESS/df)/(RSS/df) = (66,410/3)/(87,500/416) = 107.455

... which I noted can also be found with the "alternative" F-stat ..

[R^2/(k-1)] / [(1-R^2)/(n-k)] = [0.437 / (4-1)] / [(1-0.437)/(420-4)] = (0.145530781 / 0.001354345) = 107.4547069

Compare, see the link, to the restricted regression (where q = 2) where the F-stat drops to 8.010 per

Then, separately, in the exhibit below, there are homoskedastic-only F-stats = 8.010, calculated per F-stat as function of SSR (like your equation above) and R^2, restricted versus unrestricted. This is following S&W's example. These 8.01 are not a joint test of all three coefficients, but rather a joint test with only two (2) restrictions, q = 2: the joint null is that both STR and Expn are equal to zero. The F-stat of 8.01 uses as inputs either the unrestricted SSR (85,700) or unrestricted R^2 (0.437) which are produced by the overall regression.

That F-stat (i.e., of the restricted regression where q = 2) employs both regressions:

The SSR(restricted) of 89,000 and the R^2(restricted) of 0.41490 are based on TestScore = Intercept + PctEL*X1, while SSR(unrestricted) of 85,700 and the R^2(unrestricted) of 0.43659 are based on TestScore = Intercept + PctEL*X1 + Expn*X2 + STR*X3. In short, we model it again; we need two models. I hope that's helpful!