Hi @JulioFRM are you sure, it looks okay to me (although note the unusually high Rf rate assumption of 12%): if Rf = 12.0% and T = 0.25, then p = (a-d)/(u-d) = [exp(.12*0.25) - 0.9]/(1.1-0.9) = 0.130455/0.2 = 0.65227267. Let me know ... Thanks!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Errors Found in Study Materials P1.T4. Valuation & Risk Models (OLD thread)
- Thread starter Nicole Seaman
- Start date
-
- Tags
- reviewdh
- Status
- Not open for further replies.
Hi David,
this is from your Study Notes page 21 on Allen.
If K=100 how can there data points which are 165 periods ago?
I thought we have 250 data points and just look back at the 100 recent and these 100 recent data points we sort descending and do our computations on them.
So the oldest can be max. 100 periods ago?
Alphabet (Ticker: GOOG)
Exxon Mobil Corp (Ticker: XOM)
T 250
lambda, λ 0.98
K 100
Periods Hybrid (EXP)
Return Ago Weight Cumul
-5.46% 165 0.07% 0.07%
-5.06% 220 0.02% 0.10%
-3.87% 121 0.18% 0.28%
-3.58% 234 0.02% 0.29%
-3.51% 218 0.03% 0.32%
-2.94% 24 1.26% 1.58%
-2.88% 232 0.02% 1.60%
-2.66% 126 0.16% 1.76%
-2.64% 219 0.02% 1.79%
-2.41% 22 1.32% 3.11
Thank you a lot, Regards
this is from your Study Notes page 21 on Allen.
If K=100 how can there data points which are 165 periods ago?
I thought we have 250 data points and just look back at the 100 recent and these 100 recent data points we sort descending and do our computations on them.
So the oldest can be max. 100 periods ago?
Alphabet (Ticker: GOOG)
Exxon Mobil Corp (Ticker: XOM)
T 250
lambda, λ 0.98
K 100
Periods Hybrid (EXP)
Return Ago Weight Cumul
-5.46% 165 0.07% 0.07%
-5.06% 220 0.02% 0.10%
-3.87% 121 0.18% 0.28%
-3.58% 234 0.02% 0.29%
-3.51% 218 0.03% 0.32%
-2.94% 24 1.26% 1.58%
-2.88% 232 0.02% 1.60%
-2.66% 126 0.16% 1.76%
-2.64% 219 0.02% 1.79%
-2.41% 22 1.32% 3.11
Thank you a lot, Regards
Hi @QuantFFM Good catch, my mistake (apologies)! I just examined the XLS (it's in the learning sheet at https://learn.bionicturtle.com/topic/learning-spreadsheet-allen-chapters-2-3/ ). The K = 100 is not used at all; it is just mistakenly displayed on the chart. Per the text ("we retrieved daily returns for the one year ending") the historical window is 250 days. And the 250 days is used to determine the hybrid weights. For example, the worst return of -5.46% is weighted according to (1-0.98)*0.98^(165-1)/(1-0.98^25) which is a product of the typical (1-λ)*λ^(n-1) = (1-0.98)*0.98^(165-1) and 1/(1-0.98^250) which is a slight upward multiplier that "trims" the total weight of 250 (truncated from an infinite series) days from 99.36% to a full 100.0% based on the 250 day window.
Re: "I thought we have 250 data points and just look back at the 100 recent and these 100 recent data points we sort descending and do our computations on them. "
No, my "uninvited" K = 100 is maybe confusing you. There is only a historical window (in this example, the recent T = 250 daily returns). They are sorted and weighted. And you can see from the weight example above, the only inputs to the weight are the actual day (and, if we are trimming up to 100.0% which is optional, then the 250 enters). I hope that explains, thank you again!
cc @Nicole Seaman I'll need to fix this
Note 04/02/19: This has been fixed in the PDF
Re: "I thought we have 250 data points and just look back at the 100 recent and these 100 recent data points we sort descending and do our computations on them. "
No, my "uninvited" K = 100 is maybe confusing you. There is only a historical window (in this example, the recent T = 250 daily returns). They are sorted and weighted. And you can see from the weight example above, the only inputs to the weight are the actual day (and, if we are trimming up to 100.0% which is optional, then the 250 enters). I hope that explains, thank you again!
cc @Nicole Seaman I'll need to fix this
Note 04/02/19: This has been fixed in the PDF
Last edited by a moderator:
theapplecrispguy
New Member
Hi David. On Tuckman Chapter 4 -- page 74 of your notes, I cannot reconcile your spreadsheet with your description when you Compare and contrast DV01 and Duration for 2 1/8 bonds yielding 2.092%. Specifically your description in the 7th bullet on page 74 "divides by the price times one plus half the yield" and the Mac convexity description is similar. Your spreadsheet and hence the results on page 73 don't seem to include the "one plus half the yield" factor. Can you please explain. Thanks
Hi @theapplecrispguy Sorry that's just a mistake in the text (cc @Nicole Seaman ) We've somehow inserted all those extra words uggh  , it should be much simpler:
, it should be much simpler:
So it should read:
Note: This has been updated in the PDF v7
 , it should be much simpler:
, it should be much simpler:
- The Macaulay duration of the bond is the sum of the time-weighted present values ($477.7621) divided by the price (the $101.16 just being the sum of the present values)
times one plus half the yield, which is $100.2 (=101.16 × (1 + (1 + 2.092%/2). It can also be calculated directly as DV01 divided by the priceand is found to be 4.7702.- The Modified duration of the bond is found by dividing the Mac duration by one plus half the yield (4.772 / (1 + 2.092%/2) and is found to be 4.7208. It can also be calculated directly as DV01 divided by price and multiplied by 10,000: 0.0473/101.16*10,000 = 4.7208 (inputs rounded).
- The (Mac) convexity of the bond is approximately the sum of time squared weighted present values ($2347. 19) divided by price
times one plus half the yield($100.2) and is found to be 23.4354
So it should read:
- "The Macaulay duration of the bond is the sum of the time-weighted present values ($477.7621) divided by the price (the $101.16 just being the sum of the present values) and is found to be 4.7702.
- The Modified duration of the bond is found by dividing the Mac duration by one plus half the yield (4.772 / (1 + 2.092%/2) and is found to be 4.7208. It can also be calculated directly as DV01 divided by price and multiplied by 10,000: 0.0473/101.16*10,000 = 4.7208 (inputs rounded).
- The (Mac) convexity of the bond is approximately the sum of time squared weighted present values ($2347. 19) divided by price ($100.2) and is found to be 23.4354"
Note: This has been updated in the PDF v7
Last edited by a moderator:
theapplecrispguy
New Member
Thanks. When you are updating this section, I think the formula (4.772 / (1 + 2.092%/2) should read (4.7702 / (1 + 2.092%/2 )) to match your spreadsheet.
Note: This has been updated in the PDF v7
Note: This has been updated in the PDF v7
Last edited by a moderator:
Yes @theapplecrispguy certainly ... thank you again!
evelyn.peng
Active Member
Hi David,
On page 9 of the Study Notes for P1.T4 Schroeck's Chapter 14 on Capital Structure in Banks, under section "Describe how economic capital is derived",
"Step 3. Estimation of Unexpected Loss Contribution (ULC) to the lending portfolio as a function of expected loss, weight of the loan in the portfolio and its correlation with rest of the portfolio".
When I look at the formula for ULCi, I can see the weight of the loan, and the correlation to the portfolio, but I only see it as a function of unexpected loss of the loan to the portfolio, not expected loss.
Am not sure if it's a missed understanding on my part?
On a related note, do you publish videos or learning spreadsheet for Chapter 14 for P1.T4 or is it intentionally not produced? Always appreciate the rich learning content, so I thought I double check.
Thanks!
Evelyn
On page 9 of the Study Notes for P1.T4 Schroeck's Chapter 14 on Capital Structure in Banks, under section "Describe how economic capital is derived",
"Step 3. Estimation of Unexpected Loss Contribution (ULC) to the lending portfolio as a function of expected loss, weight of the loan in the portfolio and its correlation with rest of the portfolio".
When I look at the formula for ULCi, I can see the weight of the loan, and the correlation to the portfolio, but I only see it as a function of unexpected loss of the loan to the portfolio, not expected loss.
Am not sure if it's a missed understanding on my part?
On a related note, do you publish videos or learning spreadsheet for Chapter 14 for P1.T4 or is it intentionally not produced? Always appreciate the rich learning content, so I thought I double check.
Thanks!
Evelyn
evelyn.peng
Active Member
Hi, I found some youtube videos on ULCi and spreadsheet on 2 asset ULC calculation. So please ignore the latter part of my comment. Thanks,Hi David,
On page 9 of the Study Notes for P1.T4 Schroeck's Chapter 14 on Capital Structure in Banks, under section "Describe how economic capital is derived",
"Step 3. Estimation of Unexpected Loss Contribution (ULC) to the lending portfolio as a function of expected loss, weight of the loan in the portfolio and its correlation with rest of the portfolio".
When I look at the formula for ULCi, I can see the weight of the loan, and the correlation to the portfolio, but I only see it as a function of unexpected loss of the loan to the portfolio, not expected loss.
Am not sure if it's a missed understanding on my part?
On a related note, do you publish videos or learning spreadsheet for Chapter 14 for P1.T4 or is it intentionally not produced? Always appreciate the rich learning content, so I thought I double check.
Thanks!
Evelyn
Evelyn
Hi @evelyn.peng Yes I agree that the inclusion of "expected loss" is bad, when describing the steps to retrieve the unexpected loss contribution (ULC). It looks like we picked this up from Schroeck page 179, notice his first bullet (EL is implicted indirectly, but that's very confusing!):
Re: XLS for the section, it looks like we don't have a (polished) version published yet, only a staged version ... so it will be published at some point. Thanks!
I am tagging to revise this for clarity, thank you!"Therefore, considering a loan at the portfolio level, the contribution of a single UL(i) to the overall portfolio risk is a function of:
- The loan’s expected loss (EL), because default probability (PD), loss rate (LR), and exposure amount (EA) all enter the UL-equation
- The loan’s exposure amount (i.e., the weight of the loan in the portfolio)
- The correlation of the exposure to the rest of the portfolio"
Re: XLS for the section, it looks like we don't have a (polished) version published yet, only a staged version ... so it will be published at some point. Thanks!
Last edited:
Branislav
Member
Hi @Branislav Yes, absolutely the principal is missing. Apologies, our mistake. Thank you! Also, the $100.00 is missing in the coupons: the first coupon cash flow is not 0.75%/2 but rather $100.00 * 0.75%/2. cc @Nicole Seaman The highlighted formula should read:
- ($100.00 * 0.75%/2 × 0.99925) + ($100.00 * 0.75%/2 × 0.99648) + ($100.00 + $100* 0.75%/2 × 0.99648) = $100.255, or
- [(0.75%/2 × 0.99925) + (0.75%/2 × 0.99648) + ((1.0 + 0.75%/2) × 0.99648)] * $100.00 = 1.00255 * $100.00 = $100.255
Maxim Rastorguev
Member
David, referring to this video 25:50 you went to realzed forward scenario in yields. As stated this meant that previous forwards now became spot. But when you calculated new price of the bond , it seemed you still treated rates as forward, not spot. Specificaly you discounted the final bond cash flow with both first rate and second rate (see picture). But if these are all spots, shouldnt we simply apply each rate for each cash flow? 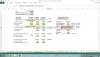

Hi @Maxim Rastorguev I mispoke (I do apologize) when I said "spot rates" plural, when I should have said singular spot rate. The Realized Forward scenario reflects the "realization" of current forward when we move forward in time. In the example shown:
- On 5/30/10, for the bond that matures in 11/31/11, there is an initial forward 1.5 year forward rate curve give by {0.193%, 0.600%, 1.080%}. Using these forward rates, it is priced at $100.190. Please note at this time, the six month forward rate, F(0.5, 0.5) = 0.60% and the one-year forward rate, F(1.0, 0.5) = 1.080%.
- Then we go forward in time six months, to 11/30/11 when the bond has only one year to mature. We can make different assumptions but the scenario assumption of Realized Forwards implies:
- The previous six-month forward rate of 0.60% becomes the six-month spot rate (note: this can also be called the six-month forward rate starting immediately)
- The previous one-year forward rate of 1.080% becomes the current six-month forward rate; hence the "realization" of the forward rates. The one-year bond (on 11/30/11) is priced with these two rates; I meant to say the 0.60% becomes the six-month spot rate, and the previous one-year forward becomes the six-month forward rate. They do not all become spot rates; rather, the pricing mechanics is exactly the same as in the initial step, we've just moved forward six months so there are only two cash flows to discount. I hope that's helpful, thanks!
Maxim Rastorguev
Member
Thank you, it is clear now!
Sixcarbs
Active Member
Amenc Chapter 4
It says under Sharpe and Jensen:
"Replacing this value of in the Jensen’s equation and dividing by σ(p) we get"
I think it should be "dividing by σ(m)."
It says under Sharpe and Jensen:
"Replacing this value of in the Jensen’s equation and dividing by σ(p) we get"
I think it should be "dividing by σ(m)."
Last edited:
Hi @Sixcarbs Actually, it currently looks correct to me:
Given Jensen's E(Rp) - rf = α + β(p,m)* E(Rm - rf),
And assuming ρ(p,m) = 1.0 in a well-diversified portfolio s.t. β(p,m) = σ(p)/σ(m):
E(Rp) - rf = α + [σ(p)/σ(m)]*E(Rm - rf). Now divide by σ(p):
[E(Rp) - rf]/σ(p) = α/σ(p) + [σ(p)/σ(m)]*E(Rm - rf)/σ(p) = α/σ(p) + [σ(p)/σ(m)]*E(Rm - rf)/σ(p) =
[E(Rp) - rf]/σ(p) = α/σ(p) + E(Rm - rf)/σ(m). Thanks,
Given Jensen's E(Rp) - rf = α + β(p,m)* E(Rm - rf),
And assuming ρ(p,m) = 1.0 in a well-diversified portfolio s.t. β(p,m) = σ(p)/σ(m):
E(Rp) - rf = α + [σ(p)/σ(m)]*E(Rm - rf). Now divide by σ(p):
[E(Rp) - rf]/σ(p) = α/σ(p) + [σ(p)/σ(m)]*E(Rm - rf)/σ(p) = α/σ(p) + [
[E(Rp) - rf]/σ(p) = α/σ(p) + E(Rm - rf)/σ(m). Thanks,
Sixcarbs
Active Member
@David Harper
Sorry, I am 1,000% wrong here. The notes are fine.
Sorry, I am 1,000% wrong here. The notes are fine.
- Status
- Not open for further replies.
Similar threads
- Sticky
- Replies
- 3
- Views
- 1K
- Sticky
- Replies
- 0
- Views
- 927
- Sticky
- Replies
- 3
- Views
- 1K
- Sticky
- Replies
- 0
- Views
- 656
- Sticky
- Replies
- 0
- Views
- 580
