Definitions of probability of default vs. cumulative or marginal probability of default

[Merlinius]

Hi, in book 2, chapter 4 (or the BT study notes), the following definitions are presented:



I do not understand how to read the second definition. [t, t+k) is a continuous set. Therefore, I do not see how the numerator is supposed to be defined here. Even if I assume that we simply iterate over all discrete subsets, say all days, how is

\[ Def_t^{t+k} \]

not the same as the numerator in the first formula?

\[ \sum_{i=t}^{t+k} DEF_i \]

I must misunderstand something, because to me both formulas show the frequency of names that default within the interval [t, t+k) (or maybe [t, t+k] because the upper boundary is clearly contained in the summation, but I have a feeling this is not the distinction de Laurentis is trying to make).

Then the confusion continues when the marginal default rate is defined as the same thing:



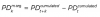
Since \[ PD_t^{\text{cumulated}} = \frac{\sum_{i=t}^{t+0} DEF_i}{Names_t} = 0 \]

according to the above definition. (I have substituted the upper boundary for t = t + 0, because I have a feeling that de Laurentis does not want the upper boundary to be t + t = 2t which would be consistent with his notation in the prior formula)

I know that there must be some inaccuracies with regard to the indexes but even trying to be lenient on the notation, I cannot make sense of these definitions, or distinguish any from the others.

 

[David Harper CFA FRM]

Hi @Merlinius de Laurentis is confused, I've told GARP that I think it's the worst reading in P2 (and it's part of the PD confusion mentioned in my memo "How to Fix the FRM" https://forum.bionicturtle.com/thre...-committee-and-garps-board-of-trustees.22758/). Since the day it was introduced into the syllabus, we've had to report multiple errors in this text and I have repeatedly asked for its removal due to the confusions created...

For your terms above, I don't want to get bogged down in his notation, but we can draw inferences from Table 3.5 because it has numbers, right? I would just say:

1. I'm not sure there is a difference between your two Def(i) above, except the former is single period and the latter is multi-period. Take his table 3.5. The annual defaults are {10, 12, 13, 15, 20). You could (unrealistically) define k = 5 years, such that the period is 5 years and the Def_i(t + 5 years) = 70. Alternatively, realistically, it's divided into five periods, the first Def_i(t+1 year) = 10. I don't see a difference here aside from time slicing; e.g., 70 is the right number both cumulative over five year, or if we want to be silly and define the 5-years as a single period.

2. PD(marginal) is the unconditional default probability and it is the difference between cumulative probabilities. In Table 3.5, the unconditional (aka, marginal) default probability during the 5th year = 5-year_cumulative PD - 4-year_cumulative PD = 7.0% - 5.0% = 2.0%. Isn't that the same as default(during year 5)/(names at t0) = 20/1,000 = 2.0%. Yes, it surely is!

So ignoring his notation, we know that it should be (or can be):

• marginal_PD during the k-th year from the perspective of today, t0, is given by marginal_PD(t, t+k)
  = cumulative_PD(0,t+k) - cumulative_PD(0,t)
• For example, marginal_PD during the 5th year from the perspective of today, t0, such that t = 4 and k = 1, is given by marginal_PD(4, 4+1) = cumulative_PD(0,4+1) - cumulative_PD(0,4) = 7.0% - 5.0% = 2.0%. I hope that's helpful!

 

[Merlinius]

Thanks, this makes a lot of sense. I got stuck on the formulas so that I did not see table 4.5.

 

[lowhueyyi]

Hi @David Harper CFA FRM ,

I know this has been ask many times in the forum but the more I search through and read, the more I am confused. I am also not sure which are the most up to date definition or errors that may have been corrected .My questions are

1. Is Marginal PD a conditional or unconditional PD? From your video [Conditional default probability (hazard rate)], I saw that you mentioned Marginal PD is a conditional PD but it seems different from the formula defined by Giacomo De Laurentis.

2. Is Forward PD the conditional PD since by definition of book 2, chapter 4 (Giacomo De Laurentis, BT study notes ), we divide marginal PD (by definition from Giacomo De Laurentis) with survival probability and it seems to be conditional?

3. Is Hazard Rate = Forward PD or Marginal PD. From the look of the formula for Forward PD, it seems like it Forward PD is the Hazard rate. Since Hazard rate is a conditional probability, does this imply Forward rate is conditional PD? The link below seems to also suggest that Hazard Rate = Forward PD.

https://www.investment-and-finance.net/risk-management/h/hazard-rate.html

4. Can I directly think that probability of default = marginal probability of default whenever i encounter only the term PD as it is being used in many section of main text book/notes?

Apologies for such a long and repetitive questions (as it has been ask many times in different threads) but I really hope I can understand it clearly. Thanks!

 

[David Harper CFA FRM]

Hi @lowhueyyi Right, it's confusing because we have different authors, as mentioned in previous post. I've summarized the important metrics in the exhibit below, with numbers to give exact clarity; XLS is here https://www.dropbox.com/s/3lb6c016ar9czn2/0813_different_pd_definitions.xlsx?dl=0

In regard to your questions:

1. Marginal PD is a term I don't like because it has two definitions. But most often is a synonym for unconditional PD (but I've occasionally seen it referenced as a synonym for conditional, so I really don't like it!). In the FRM, we could say that unconditional PD = marginal PD, but I much prefer to settle on unconditional PD because I think it's rather unambiguous and perfectly descriptive: it is the PD from the perspective of today; i.e., not conditional on survival forward in time. (My exhibit does include Malz's definition of Marginal PD, as a first derivative, which is less often used and for our purposes, it is esoteric and unimportant).
2. De Laurentis's forward PD is the same as conditional PD but it's uncommon usage in the FRM; eg, forward PD should never appear on the exam).
3. Hazard rate (aka, default intensity) is an instantaneous conditional default probability. In my exhibit below, the hazard rate is the only input at 9.0%, and as expected, the conditional PD is nearby at 8.6% but it's not the same because the 8.6% conditional PD is not instantaneous, it is the default probability during the third year (a one year horizon) conditional on survival up to the beginning of the third year. Put another way, the numerator in the 8.6% conditional PD is not instantaneous, it refers to a one year horizon.
4. In my opinion, "probability of default" by itself is not enough, and our feedback to GARP reflects this. Too often is it misinterpreted. I will say, by itself it usually refers to a conditional PD. But we've given GARP many examples of why it's best to include the appropriate adjective (including in my referenced memo, you can see concrete references). That said, the context is often enough. The first thing to do is pay attention to the context, which often will tell you.
5. In short, I think we should care about these three (four including hazard) terms:
   • Cumulative default/survival (happily, no synonyms!)
   • Conditional PD (sure "forward" is a synonym but we won't see it ...)
     • And realize hazard rate (default intensity) is a special case of conditional default when the time horizon is really short!
   • Unconditional PD. I hope that's helpful!

 

[lowhueyyi]

Hi @David Harper CFA FRM I have just read through the topic spread risk and default intensity models by Malz. Can I ask a little bit more which may help to clear my confusion? For ECL calculation the formula always include PD but which PD are we referring to ? (Marginal, forward , unconditional , conditional default probabilities, hazard). I guess it is marginal? But I am not really confident with that answer. Using the above excel as example, assuming we have the LGD and EAD for year 2, which PD will be used for calculating ECL?

Secondly, just one question which may be out of scope of FRM but I wish to link what I learn to real application. I always saw that ifrs9 mentioned using 12 month pd (forward looking) or lifetime pd to calculate ECL. But my main concern is the 12 month pd. I am not sure which PD does it refer to. Is it referring to sum of marginal PD for 12 months which is part of Cumulative PD? Or Sum of forward conditional pd for 12 months? Or sum of all 12 months hazard rate instantaneous conditional PD?

Lastly, is marginal pd the same as the joint event pd obtained from
P (survive up to time =1 and survive at t=2)
=p(survive up to t=1)*p(default at t=2|survive up to t=1)
assuming two period? Can I safely assume that the conditional probability above is the forward [just like the case of forward rate where (1+r(1)/2)^2=(1+r(0.5)/2)*(1+f(1)/2)]?

Thanks!

 

[David Harper CFA FRM]

Hi @lowhueyyi So I guess you saw my response. Your last question is the easiest (although I guess you just edited it ....)

• The joint default probability is the same as unconditional (be definition); in the example above, the year 3 unconditional PD of 7.2% (final column, one row up from bottom) is the same as the joint probability (survive first two years ∩ default during third year) = Pr(Cumul Survival 2 years) = 83.5% * PR(Conditional Prob Default 8.6% in third year = 8.6% = 7.2%. So, I am going to avoid "marginal" because it has two meanings. But Unconditional Prob(default in Year x) = Joint Probability (Survive to end of year X -1 ∩ Conditional default during year X) ... I see you added the forward rate analogy; yea, I get why you did that, reasonable, but I am reluctant to make this analogy. 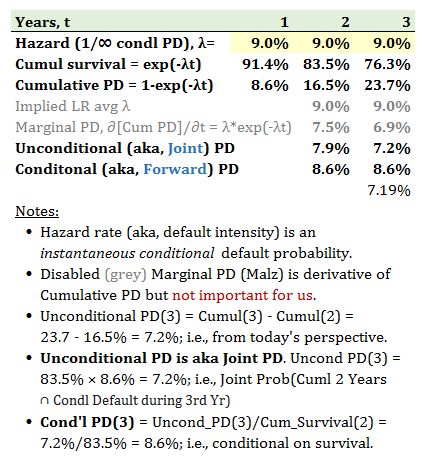I don't want to defend it later I created the XLS exhibit above to be as simple as possible yet to concretely define these terms, I don't think it needs to be oversold with analogies.

Re: ECL, I am actually not certain which is used (under IFRS9), sorry. I prefer not to generalize given i have not seen an actual use case (this is why the definitions are important). In the first Year 1 (i.e., next 12 months) it obviously doesn't matter (i.e., cumulative PD = conditional PD = unconditional PD in year 1). Put another way, when the measure refers to "within the first period (of any duration; eg, 12 months)," there is no dilemma! But I hesitate to generalize w.r.t. forward PDs because (i) I tend to agree with you that theoretically the unconditional is (often) appropriate but (ii) in practice, I am quite confident that everybody tends to use conditional PDs. Transition matrices are conditional PD (as above, hazard rates are a special case of conditional PDs). When in doubt, and when specifics are not provided, and you want to go with the crowd, it is probably wise and best to assume conditional PDs. (although we do need to be careful, it's not the exact same application but I had to repeatedly explain to GARP why they were wrong to be using conditional PDs in their CVA when it should be unconditional PDs https://forum.bionicturtle.com/threads/garp-2017-p2-76.10344 ... so it really does depend on context).

Of course you are correct that ECL wants 12-month and lifetime PDs, but I'll need to refresh my understanding of IFRS before I can be definitive ... I wrote a couple of questions last year (see https://forum.bionicturtle.com/thre...n-ifrs-9-iasb-and-gaap-fasb-cecl-cohen.13427/ and https://forum.bionicturtle.com/thre...it-loss-models-in-ifrs9-iasb-gaap-fasb.13436/) based on last year's 2018 assigned T9 current issue reading, which did cover ECL (i.e., "The new era of expected credit loss provisioning") but I don't think it settles your question. Thanks,

 

[David Harper CFA FRM]

Hello thread. Because @lowhueyyi raised a great point about the "Joint PD," I edited the exhibit (see below) to include the fact that Joint PD = Unconditional PD (including see footnote). Further I deleted Marginal as a synonym for Unconditional, the problem is: I can find uses of "marginal" that refer to both conditional and unconditional (actually, if you are keeping count, we can identify three definitions for marginal PDs if you include the derivative). I am retaining Forward (as synonym to Conditional) because I can see it has ample academic precedent ...

Therefore, I am going to continue my plan of discouraging the use of marginal simply because it seems to be confusing. I think the best terms are: cumulative, conditional, and unconditional (aka, joint). Thank you! Link to XLS is https://www.dropbox.com/s/3lb6c016ar9czn2/0813_different_pd_definitions.xlsx?dl=0