Kavita.bhangdia
Active Member
Hi David,
Please can you help me with this problem.
I am struggling with how do I take the confidence interval into consideration while calculating the CVAR.
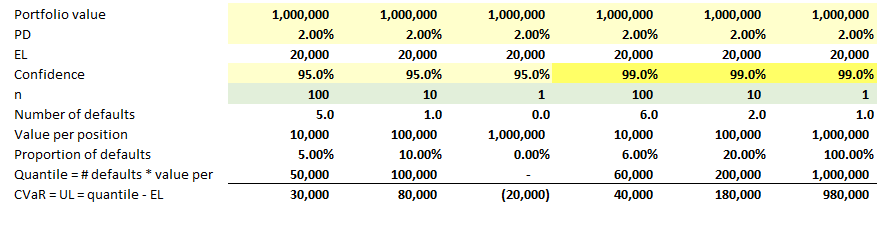
A portfolio has n credit, total portfolio value is 1,0000,000.
The probability of default is 2% for each credit. Assume zero recovery and default correlation is 1.
Find the CVAR at 95% confidence interval.
Solution
My expected loss =.02*1000000= 20000
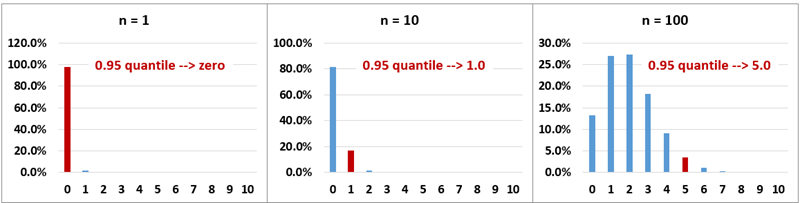
My credit loss at 95% is zero. So my Cvar is -20000
Is it correct??
What will be my Cvar at 99% confidence.
Please can you help me with this problem.
I am struggling with how do I take the confidence interval into consideration while calculating the CVAR.
A portfolio has n credit, total portfolio value is 1,0000,000.
The probability of default is 2% for each credit. Assume zero recovery and default correlation is 1.
Find the CVAR at 95% confidence interval.
Solution
My expected loss =.02*1000000= 20000
My credit loss at 95% is zero. So my Cvar is -20000
Is it correct??
What will be my Cvar at 99% confidence.