WhizzKidd
Member
Hi @David Harper CFA FRM
I am trying to understand the credit exposure profiles in Ch13.
For an IRS (Pay Fix, Recieve Float):
The scenario in the notes where i_fix>i_flt initially, then reverses afterward, as the yield curve slopes upwards. Why initially when I am paying net on the swap the credit exposure is positive and not below 0 instead? Because credit risk is when money is owed to me and the counterparty may default, which makes sense when I am receiving net on the swap (when i_flt>i_fix), but not in the former case. Or another way, if MTM=PV(received cashflows)-PV(Paid cashflows), if i_fix(paid) < i_float, then PV (paid)>PV (received), which implies a (-MTM), which is when there is no credit risk. Am I understanding this right?
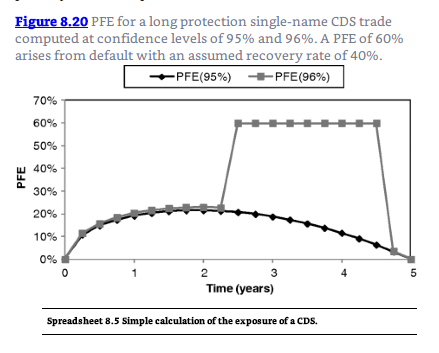
For a CDS (Long CDS):
It says the exposure profile is positive since the credit spread may widen. Again we are paying the spread, and the exposure on a CDS is when we don't receive the payout at default. Is it because the MTM of the CDS is becoming greater since we locked in an initial spread lower than what the market is telling us it is now (as it widens)? So the MTM becomes more positive over time, hence greater credit risk?
I think I am a bit confused on why the profile is >0 when I am paying on the instrument.
I am trying to understand the credit exposure profiles in Ch13.
For an IRS (Pay Fix, Recieve Float):
The scenario in the notes where i_fix>i_flt initially, then reverses afterward, as the yield curve slopes upwards. Why initially when I am paying net on the swap the credit exposure is positive and not below 0 instead? Because credit risk is when money is owed to me and the counterparty may default, which makes sense when I am receiving net on the swap (when i_flt>i_fix), but not in the former case. Or another way, if MTM=PV(received cashflows)-PV(Paid cashflows), if i_fix(paid) < i_float, then PV (paid)>PV (received), which implies a (-MTM), which is when there is no credit risk. Am I understanding this right?
For a CDS (Long CDS):
It says the exposure profile is positive since the credit spread may widen. Again we are paying the spread, and the exposure on a CDS is when we don't receive the payout at default. Is it because the MTM of the CDS is becoming greater since we locked in an initial spread lower than what the market is telling us it is now (as it widens)? So the MTM becomes more positive over time, hence greater credit risk?
I think I am a bit confused on why the profile is >0 when I am paying on the instrument.