wrongsaidfred
Member
Hi David,
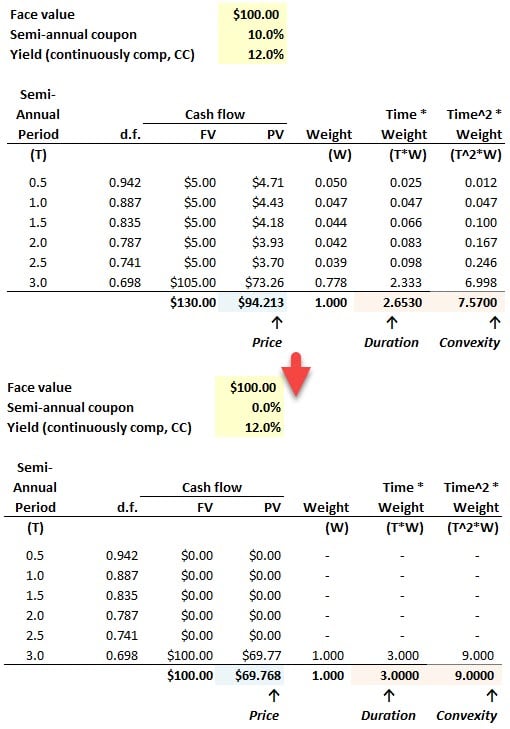
Hull has a statement about convexity that does not seem to agree with what you have. You state that convexity will decrease as the coupon increases.
Hull says "the convexity of a bond portfolio tends to be greatest when the portfolio provides payments evenly over a long period of time. It is least when payments are concentrated around one point in time." To me, it seems like a high coupon would be like spreading the payments out more evenly. In other words, according to Hull it seems like a high coupon (which would lead to a more even distibution of payments) would lead to higher convexity. Am I thinking about this completely incorrectly?
Also, with a question like this, aren't there some secondary effects we must also consider, like how a high coupon bond would have a higher price and therefore a lower yield than a low coupon bond?
For instance, a bond with an 8% coupon will be more expensive, and have a lower yield, than a bond with a 4% coupon. How do these effects net out as far as duration and convexity are concerned? In other words, a higher coupon will lead to a lower yield. A higher coupon is supposed to lead to a lower duration and convexity while a lower yield will lead to a higher duration and convexity.
Sorry for the long question. Any explanation would be greatly appreciated.
Thanks,
Mike
Hull has a statement about convexity that does not seem to agree with what you have. You state that convexity will decrease as the coupon increases.
Hull says "the convexity of a bond portfolio tends to be greatest when the portfolio provides payments evenly over a long period of time. It is least when payments are concentrated around one point in time." To me, it seems like a high coupon would be like spreading the payments out more evenly. In other words, according to Hull it seems like a high coupon (which would lead to a more even distibution of payments) would lead to higher convexity. Am I thinking about this completely incorrectly?
Also, with a question like this, aren't there some secondary effects we must also consider, like how a high coupon bond would have a higher price and therefore a lower yield than a low coupon bond?
For instance, a bond with an 8% coupon will be more expensive, and have a lower yield, than a bond with a 4% coupon. How do these effects net out as far as duration and convexity are concerned? In other words, a higher coupon will lead to a lower yield. A higher coupon is supposed to lead to a lower duration and convexity while a lower yield will lead to a higher duration and convexity.
Sorry for the long question. Any explanation would be greatly appreciated.
Thanks,
Mike