@David Harper CFA FRM
Can you explain why the Conditional Mean for an MA(1) is not 0? I see the explanation in the previous chapter regarding:
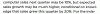
This makes sense. But, if that was the case, then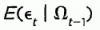 would not be 0 correct? The below seems to indicate to me that
would not be 0 correct? The below seems to indicate to me that 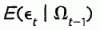 =0 and that
=0 and that 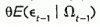 =
=  .
.
I don't really understand this.
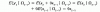
Can you explain why the Conditional Mean for an MA(1) is not 0? I see the explanation in the previous chapter regarding:
This makes sense. But, if that was the case, then
I don't really understand this.
