Hi @David Harper CFA FRM ,
Gregory, Chapter 12: Default Probabilities, Credit Spreads, Funding Costs
In your notes under the above topic, there is a sub-topic "Describe credit default swaps (CDS) and their general underlying mechanics" in this there you explained about how in recent times auctions are done, namely Big Bang Protocol, to solve earlier problems of CDS settlement. can you please explain a bit how this auction helps in solving the issue?
Also, what the meaning of delivery squeeze? In the below image you have written that the impact of delivery squeeze can be seen .....
Thanks in advance.
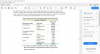
Gregory, Chapter 12: Default Probabilities, Credit Spreads, Funding Costs
In your notes under the above topic, there is a sub-topic "Describe credit default swaps (CDS) and their general underlying mechanics" in this there you explained about how in recent times auctions are done, namely Big Bang Protocol, to solve earlier problems of CDS settlement. can you please explain a bit how this auction helps in solving the issue?
Also, what the meaning of delivery squeeze? In the below image you have written that the impact of delivery squeeze can be seen .....
Thanks in advance.


