[email protected]
New Member
Hi,
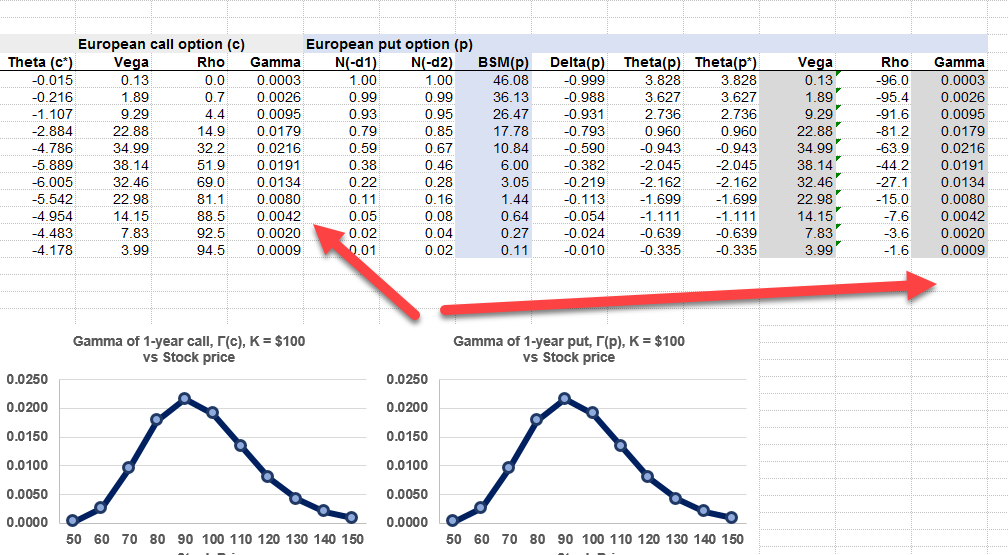
I am beating my head around this. I have seen certain atm options whenre Gamma is greater than 1? I felt if delta is bounded between 0 and 1, so should gamma?
I am beating my head around this. I have seen certain atm options whenre Gamma is greater than 1? I felt if delta is bounded between 0 and 1, so should gamma?