gargi.adhikari
Active Member
https://learn.bionicturtle.com/topic/instructional-video-hull-chapter-4/
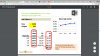
In reference to the chapter above, Please refer the screenshot below (also attached). Can someone breakdown the calculation of the Discount Factor Column for me -circled in red. I tried to plug in values into both e ^ -(rt) as well as 1/ ( 1 + r/m ) ^ mt
I am getting values of the discount factor as .9753 instead of a .942....am doing something wrong here ... Appreciate all the help on this...
Appreciate all the help on this...
In reference to the chapter above, Please refer the screenshot below (also attached). Can someone breakdown the calculation of the Discount Factor Column for me -circled in red. I tried to plug in values into both e ^ -(rt) as well as 1/ ( 1 + r/m ) ^ mt
I am getting values of the discount factor as .9753 instead of a .942....am doing something wrong here ...
 Appreciate all the help on this...
Appreciate all the help on this...


 !
!