Calculating the Premium Payable

[SPate5068]

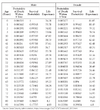
Hi all,

I was wondering if you could please help with understanding the example, I understand how to calculate the expected payout and from this the present value of payout, but I don't understand what Y is, what the emboldened formula means and where the value 1.959793 comes from. To summarise, I'm not understanding how to calculate breakeven annual premium in the last emboldened line. I've attached the mortality table for reference.

EXAMPLE: Breakeven Premium Payments
The relevant interest rate for insurance contracts is 3% per annum (semiannual compounding applies), and all premiums are paid annually at the beginning of the year. A $500,000 term insurance contract is being proposed for a 60-year-old male in average health. Assuming that payouts occur halfway throughout the year, calculate the insurance company’s breakeven premium for a one-year term and a two-year term.

Answer:

One-year term:

The expected payout for a one-year term is 0.011197 × $500,000 = $5,598.50. Assuming the payout occurs in six months, the breakeven premium is: $5,598.50 / 1.015 = $5,515.76.

Two-year term:

The expected payout for a two-year term is the sum of the expected payouts in both the first year and the second year. The probability of death in the second year is (1 − 0.011197) × 0.012009 = 0.011874, so the expected payout in the second year is 0.011874 × $500,000 = $5,937.27. If the payout occurs in 18 months, then the present value is $5,937.27 / (1.015)^3 = $5,677.91. The total present value of the payouts is then $5,515.76 + $5,677.91 = $11,193.67.

The first premium payment occurs immediately (i.e., beginning of the first year) so it is certain to be received. However, the probability of the second premium payment being made at the beginning of the second year is the probability of not dying in the first year, which is 1 − 0.011197 = 0.988803. The present value of the premium payments (using Y as the breakeven premium) = Y + (0.988803Y / 1.015^2) = 1.959793Y.

Computing the breakeven annual premium equates the present value of the payouts and the premium payments as follows: 11,193.67 = 1.959793Y. Solving for Y, the breakeven annual premium is $5,711.66.

 

[David Harper CFA FRM]

Hi @SPate5068 The key idea to the solution is that the PV(expected premium payments by the insurance customer) = PV(expected payouts by the company). It's the same equality we find in credit defaults swaps (CDS): PV(expected payments) = PV(expected payouts). In addition to discounted each payment/payout series, we are weighting them by the probability (hence the "expected').

The mortality table that you attached enables us to compute the present value of the expected payout by the insurance customer. As the solution shows, there is no need for the variable Y to compute this PV, it is given by $5,515.76 + $5,677.91 = $11,193.67 where each is an "expected discounted" value; e.g., $5,667.91 from the insurance company's perspective is an unconditional 1.1875% probability (= 98.880% survive first years * 1.2009% die in second) of paying $500,000 discounted by 1.5% ( =3% * 0.5).

We want to solve for the constant premium paid over the next two years that has the same present value, so we want Y that achieves:
1st Year: Y
2nd Year: Y * (1-0.011197) / 1.015^2
= 1.959793*Y

Notice that's almost 2*Y because the first premium (=Y) is not discounted (i.e., paid immediately) and the second premium is very likely to get paid by the customer (i.e., because he has only an 1.1197% probability of dying!). If Y = $5.711.66, then the expected discounted value of the two premium payments is given by:
$5,711.66 certain and immediate +
$5,711.66 * 98.880% / 1.015^2
= $5,711.66 + $5,482.01 = $11,193.67

Both counterparties (customer and company) are discounting two expected payment/payoff streams. The company has a very low probability of ever paying the $500,000 but the customer is almost certain to pay the premium ($5,711.66) which we solved for by setting the PV of both streams equal to each other.

I hope that explains!

 

[SPate5068]

Hi David, this explanation is great. Thank you for taking the time!