Hi All, Preparing for the Part-1 2015 Nov. Got a question on distributions from the below two questions given in the Miller's question at the end of Distributions (page 89, Q1 & Q2)
My Confusion: This is solved by Bernoullis distribution. Why can't we use poisons distribution to solve these?
Question 1:
XYZ Corporation announces its earnings four times per year. Based on historical data, you estimate that in any given quarter the probability that XYZ Corporation’s earnings will exceed consensus estimates is 30%. Also, the probability any other quarter. What is the probability that XYZ Corporation will exceed estimates three times in a given year?
Answer:
The number of times XYZ Corporation exceeds consensus estimates follows a binomial distribution; therefore:

Question 2:
The market risk group at your firm has developed a value at risk (VaR) model. In Chapter 7 we examine VaR models more closely. In the meantime, assume the probability of an exceedance event on any given day is 5%, and the probability of an exceedance event occurring on any given day is independent of an exceedance event having occurred on any previous day. What is the probability that there are two exceedances over 20 days?
Answer: The number of exceedance events follows a binomial distribution; therefore:
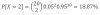
Thanks in Advance
My Confusion: This is solved by Bernoullis distribution. Why can't we use poisons distribution to solve these?
Question 1:
XYZ Corporation announces its earnings four times per year. Based on historical data, you estimate that in any given quarter the probability that XYZ Corporation’s earnings will exceed consensus estimates is 30%. Also, the probability any other quarter. What is the probability that XYZ Corporation will exceed estimates three times in a given year?
Answer:
The number of times XYZ Corporation exceeds consensus estimates follows a binomial distribution; therefore:
Question 2:
The market risk group at your firm has developed a value at risk (VaR) model. In Chapter 7 we examine VaR models more closely. In the meantime, assume the probability of an exceedance event on any given day is 5%, and the probability of an exceedance event occurring on any given day is independent of an exceedance event having occurred on any previous day. What is the probability that there are two exceedances over 20 days?
Answer: The number of exceedance events follows a binomial distribution; therefore:
Thanks in Advance
