nicholasjalonso
New Member
In the following GARP 2020 Practice Exam question #65, we use the Poisson process for defaults at 1 and 0.
65. An analyst on the fixed-income trading desk observed that the number of defaults per year in the bond portfolio follows a Poisson process. The average number of defaults is four per year. Assuming defaults are independent, what is the probability that there is at most one default next year?
A. 6.58%
B. 7.33%
C. 9.16%
D. 25.00%
Correct Answer: C
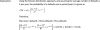
As a general (and maybe dumb math) question, how do we get 0 in the denominator as equal to 1 which you then multiple by e^-4. I always was taught in math, by definition, that a denominator of 0 is undefined and not possible.
Thanks - just tying up some loose ends before my exam Saturday! You've been so helpful David
65. An analyst on the fixed-income trading desk observed that the number of defaults per year in the bond portfolio follows a Poisson process. The average number of defaults is four per year. Assuming defaults are independent, what is the probability that there is at most one default next year?
A. 6.58%
B. 7.33%
C. 9.16%
D. 25.00%
Correct Answer: C
As a general (and maybe dumb math) question, how do we get 0 in the denominator as equal to 1 which you then multiple by e^-4. I always was taught in math, by definition, that a denominator of 0 is undefined and not possible.
Thanks - just tying up some loose ends before my exam Saturday! You've been so helpful David
Last edited by a moderator:
