AR and MA - GARP and BT notations

[frenchmarmot]

Hello,

Reviewing the available material on both MA and AR, which is in my view on of the more abstract concepts in the quant topic, I found a difference in the definition between GARP's book and the BT notes. In addition to simply having different notations (GARP use a notation for regressions that was not familiar to me but still made sense), I don't understand how it relates to the same concept.

AR(1)
=> GARP (p163 FRM Part I Quantitative Analysis, GARP) writes that AR(1) can be written as :

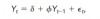
Then, the unconditional mean is stated as being dependent on the intercept.

=> In the BT notes we have :

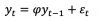
Here, I get that the same unconditional mean is 0, pointing to an intercept that in basically 0.

Question : Does GARP add an intercept so the equation looks more like a regression, but in reality it's always zero ? I don't really get the rational behind the difference in notations.


Same question for MA(1)
=> GARP (p169 FRM Part I Quantitative Analysis, GARP) writes that MA(1) can be written as :


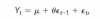
=> In the BT notes we have :

Again, GARP have an additional intercept variable that is not stated as being zero.

Question : Does GARP add an intercept so the equation looks more like a regression, but in reality it's always zero ? I don't really get the rational behind the difference in notations.

Thanks in advance for any clarification that you guys could provide me.

Greg

 

[David Harper CFA FRM]

Hi Greg (@frenchmarmot ) I bookmarked your good question until we publish the new Time Series notes (I've already drafted them). The current note is based on 2019 assigned Deibold and I did notice notational shifts, but the models were the same ... briefly, if the only difference in GARP's new edition is that they added an intercept to an ARMA-type models, this would merely be due to an author switch: AR or MA can be represented with our without the intercept (a constant). To omit is to render the "zero-mean" version but the intercept adds no value to the dynamics of an AR/MA model; i.e., the with-intercept version generalizes the model that can be accessed by a simple first-differencing. I think I recall that our revised notes, to match GARP's new notes, will include the intercept and IMHO this is the better approach as it makes no (implicit) assumption that the intercept is zero. I'll come back after we publish our note on this. Thanks!