Learning objectives: Define, calculate, and distinguish between the following portfolio VaR measures: diversified and undiversified portfolio VaR, individual VaR, incremental VaR, marginal VaR, and component VaR. Explain the impact of correlation on portfolio risk.
Questions:
21.5.1. Patricia manages a two-asset $2.0 million portfolio which is equally weighted between a Technology and Real Estate position. She assumes the returns have a multivariate (joint) normal distribution. In the exhibit below, for each position the following are displayed: size, volatility, individual value at risk (VaR) with 95.0% confidence, and marginal VaR. The portfolio's (¶) volatility and diversified VaR are also shown. (The VaR horizon is not given, but we can assume any single period; e.g., one day, one month).

What is nearest to the 95.0% component VaR of the Technology position?
a. $315,300
b. $446,595
c. $530,000
d. $750,700
21.5.2. Doug manages a two-asset portfolio with a value of $1.30 million; the portfolio holds $500,000 in a Financial fund and $800,000 in an Energy fund. He assumes the returns have a multivariate (joint) normal distribution. For each position, the following are displayed: size, volatility, individual value at risk (VaR) with 95.0% confidence, and marginal VaR. The portfolio's (¶) volatility and diversified VaR are also shown. (The VaR horizon is not given, but we can assume any single period; one day, one month).

What is nearest to the incremental VaR of the Financial Position?
a. $184,900
b. $194,011
c. $250,700
d. $433,753
21.5.3. Mary manages a two-asset portfolio with a value of $400,000; the portfolio holds $100,000 in the Materials sector (via ETF) and $300,000 in the Consumer sector. She assumes the returns have a multivariate (joint) normal distribution. For each position, the following are displayed: size, volatility, individual value at risk (VaR) with 95.0% confidence, and marginal VaR. The portfolio's (¶) volatility is also shown. (The VaR horizon is not given, but we can assume any single period; one day, one month).
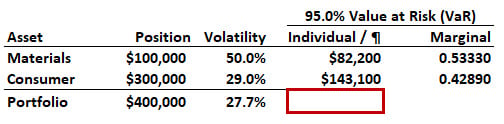
If the correlation between the positions, ρ = 0.250, what is nearest to the 95.0% confident diversified Portfolio VaR?
a. $165,000
b. $182,000
c. $225,300
d. $319,118
Answers here:
Questions:
21.5.1. Patricia manages a two-asset $2.0 million portfolio which is equally weighted between a Technology and Real Estate position. She assumes the returns have a multivariate (joint) normal distribution. In the exhibit below, for each position the following are displayed: size, volatility, individual value at risk (VaR) with 95.0% confidence, and marginal VaR. The portfolio's (¶) volatility and diversified VaR are also shown. (The VaR horizon is not given, but we can assume any single period; e.g., one day, one month).

What is nearest to the 95.0% component VaR of the Technology position?
a. $315,300
b. $446,595
c. $530,000
d. $750,700
21.5.2. Doug manages a two-asset portfolio with a value of $1.30 million; the portfolio holds $500,000 in a Financial fund and $800,000 in an Energy fund. He assumes the returns have a multivariate (joint) normal distribution. For each position, the following are displayed: size, volatility, individual value at risk (VaR) with 95.0% confidence, and marginal VaR. The portfolio's (¶) volatility and diversified VaR are also shown. (The VaR horizon is not given, but we can assume any single period; one day, one month).

What is nearest to the incremental VaR of the Financial Position?
a. $184,900
b. $194,011
c. $250,700
d. $433,753
21.5.3. Mary manages a two-asset portfolio with a value of $400,000; the portfolio holds $100,000 in the Materials sector (via ETF) and $300,000 in the Consumer sector. She assumes the returns have a multivariate (joint) normal distribution. For each position, the following are displayed: size, volatility, individual value at risk (VaR) with 95.0% confidence, and marginal VaR. The portfolio's (¶) volatility is also shown. (The VaR horizon is not given, but we can assume any single period; one day, one month).

If the correlation between the positions, ρ = 0.250, what is nearest to the 95.0% confident diversified Portfolio VaR?
a. $165,000
b. $182,000
c. $225,300
d. $319,118
Answers here:
Last edited by a moderator:
