Learning objectives: Explain the process of model validation and describe best practices for the roles of internal organizational units in the validation process. Compare qualitative and quantitative processes to validate internal ratings and describe elements of each process. Describe challenges related to data quality and explain steps that can be taken to validate a model’s data quality. Explain how to validate the calibration and the discriminatory power of a rating model.
Questions:
(Reference: Giacomo De Laurentis, Renato Maino, Luca Molteni, Developing, Validating and Using Internal Ratings (Hoboken, NJ: John Wiley & Sons, 2010))
20.4.1. Peter is a risk analyst who seeks to validate his bank's default probability (PD) estimates. His bank's large historical sample includes several years of PD estimates and the actual (aka, observed) default rates. As De Laurentis writes, "validating calibration means analyzing differences between forecasted PDs and realized default rates." In regard to possible credit rating validation methodologies, each of the following statements is true EXCEPT which is false?
a. The binomial test can be applied to one rating category at a time but it assumes independence of default events
b. The chi-square test can be used to check several rating categories simultaneously but assumes independence and a normal approximation
c. The normal test is a multi-period test of a default probability forecast for a single rating category that allows for cross-sectional dependence
d. The traffic lights approach cannot be applied to the validation of PD estimates because it is designed for the backtest of value at risk (VaR) models
20.4.2. Consider the credit rating migration matrix below:
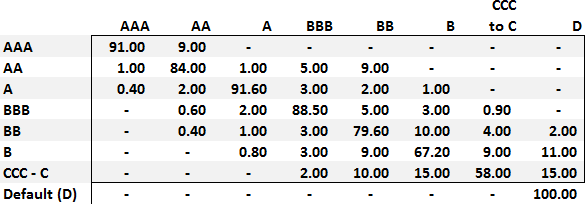
This matrix contains an abnormality (i.e., a property that is not desirable). Where is the abnormality?
a. The AA row contains an abnormality
b. The diagonal contains an abnormality
c. The BBB row contains an abnormality
d. The default column, (D), contains an abnormality
20.4.3. A bank employs a credit rating score and a cutoff value in order to make loan decisions to potential borrowers. The image below illustrates the hypothetical distribution of rating scores (X-axis) for defaulting and non-defaulting debtors (source: Studies on the Validation of Internal Rating Systems, Basel Committee on Banking Supervision, Working Paper No. 14):
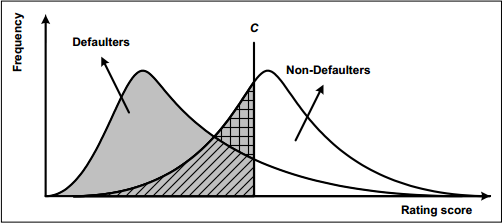
The vertical line (C) is the bank's cutoff. In order to validate the discriminatory power of its credit rating system, the bank also utilizes a cumulative accuracy profile (CAP) and receiver operating characteristic (ROC) curve. In regard to this bank's system, each of the following statements is true EXCEPT which is false?
a. Either a CAP or ROC curve can be constructed from the distributional data
b. The above does not illustrate a perfect model but a perfect ROC or CAP model has a score of one; i.e., a ROC AUC of 1.0 or a CAP accuracy ratio (AR) of 1.0
c. If the rating model were unrealistically perfect, then the two distributions (i.e., defaulters versus non-defaulters) would perfectly overlap and appear as a single distribution
d. If the bank wants to reduce the probability of mistakenly lending to a defaulter it should increase the cutoff value, but this will also increase the probability of avoiding (i.e., not lending to) a non-defaulter
Answers here:
Questions:
(Reference: Giacomo De Laurentis, Renato Maino, Luca Molteni, Developing, Validating and Using Internal Ratings (Hoboken, NJ: John Wiley & Sons, 2010))
20.4.1. Peter is a risk analyst who seeks to validate his bank's default probability (PD) estimates. His bank's large historical sample includes several years of PD estimates and the actual (aka, observed) default rates. As De Laurentis writes, "validating calibration means analyzing differences between forecasted PDs and realized default rates." In regard to possible credit rating validation methodologies, each of the following statements is true EXCEPT which is false?
a. The binomial test can be applied to one rating category at a time but it assumes independence of default events
b. The chi-square test can be used to check several rating categories simultaneously but assumes independence and a normal approximation
c. The normal test is a multi-period test of a default probability forecast for a single rating category that allows for cross-sectional dependence
d. The traffic lights approach cannot be applied to the validation of PD estimates because it is designed for the backtest of value at risk (VaR) models
20.4.2. Consider the credit rating migration matrix below:

This matrix contains an abnormality (i.e., a property that is not desirable). Where is the abnormality?
a. The AA row contains an abnormality
b. The diagonal contains an abnormality
c. The BBB row contains an abnormality
d. The default column, (D), contains an abnormality
20.4.3. A bank employs a credit rating score and a cutoff value in order to make loan decisions to potential borrowers. The image below illustrates the hypothetical distribution of rating scores (X-axis) for defaulting and non-defaulting debtors (source: Studies on the Validation of Internal Rating Systems, Basel Committee on Banking Supervision, Working Paper No. 14):

The vertical line (C) is the bank's cutoff. In order to validate the discriminatory power of its credit rating system, the bank also utilizes a cumulative accuracy profile (CAP) and receiver operating characteristic (ROC) curve. In regard to this bank's system, each of the following statements is true EXCEPT which is false?
a. Either a CAP or ROC curve can be constructed from the distributional data
b. The above does not illustrate a perfect model but a perfect ROC or CAP model has a score of one; i.e., a ROC AUC of 1.0 or a CAP accuracy ratio (AR) of 1.0
c. If the rating model were unrealistically perfect, then the two distributions (i.e., defaulters versus non-defaulters) would perfectly overlap and appear as a single distribution
d. If the bank wants to reduce the probability of mistakenly lending to a defaulter it should increase the cutoff value, but this will also increase the probability of avoiding (i.e., not lending to) a non-defaulter
Answers here:
