Learning objectives: Explain how to implement and maintain a delta-neutral and a gamma-neutral position. Describe the relationship between delta, theta, gamma, and vega.
Questions:
820.1. Trader Joe (who is unrelated to the awesome grocery store!) takes a long position in 100 out-of-the-money (OTM) put option contracts when the non-dividend-paying stock price is $88.00 and its volatility is 28.0%; each contract is for 100 options. The strike price is $80.00 and the option term is six months. The risk-free rate is 5.0%. The value of each option is $4.38 and the position's value is $43,800.00. With respect to these puts, the immediate percentage delta, Δ = -0.2550 and gamma, Γ = 0.0130. If the stock price jumps by +$7.00 to $95.00, which is nearest to the position's value as approximated by delta and gamma; i.e., without a full re-pricing of the position?
a. $18,280
b. $25,950
c. $29,135
d. $33,640
820.2. Springshield is a market maker who has written a straddle for a client; this is a "top straddle" or "straddle write" which entails selling a call and a put with the same exercise price and expiration date. While the stock price is $90.00, the options' strike price is also $90.00 and the maturity is 20 days. The stock's volatility is 18.0% and the riskless rate is 4.0%. The straddle write includes 100 option contracts, and each contract is on 100 options. The position is almost delta neutral; aka, the position delta is effectively zero. When the option maturity is twenty days, the market maker's initial position theta is 228,678 and its position gamma is -1,735. If nothing else changes (i.e., ceteris paribus such that the stock price, volatility, and riskfree rate are unchanged), what happens to market maker's position theta and gamma after ten days later, when the option maturity is only ten days?
a. Both position theta and position gamma increase
b. Position theta increases and position gamma decreases
c. Position theta decreases and position gamma increases
d. Both position theta and position gamma decrease
820.3. Consider a portfolio that is delta neutral, with a gamma of -200 and a vega (measuring sensitivity to implied volatility) of -5,000. The options shown in the following table can be traded. The portfolio can be made vega neutral by including a long position in 125 of Option 2. This would alter position delta to -48.75 and require that about 49 units of the asset be purchased to maintain delta neutrality. The gamma of the portfolio would change from -200.0 to -168.75.
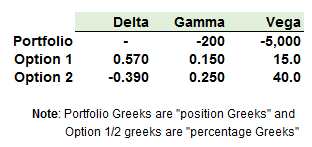
Which trade(s) will neutralize delta, gamma and vega? (this is a variation on Hull's example 19.5)
a. Short 1,333 of Option 1; Short 4,750 of Option 2; plus Long 800 of the underlying asset
b: Short 900 of Option 1; Long 2,000 of Option 2; plus Long 390 of the underlying asset
F: Long 1,650 of Option 1; Long 700 of Option 2; plus Short 500 of the underlying asset
d. Long 3,000 of Option 1; Short 1,000 of Option 2; plus Short 2,100 of the underlying asset
Answers here:
Questions:
820.1. Trader Joe (who is unrelated to the awesome grocery store!) takes a long position in 100 out-of-the-money (OTM) put option contracts when the non-dividend-paying stock price is $88.00 and its volatility is 28.0%; each contract is for 100 options. The strike price is $80.00 and the option term is six months. The risk-free rate is 5.0%. The value of each option is $4.38 and the position's value is $43,800.00. With respect to these puts, the immediate percentage delta, Δ = -0.2550 and gamma, Γ = 0.0130. If the stock price jumps by +$7.00 to $95.00, which is nearest to the position's value as approximated by delta and gamma; i.e., without a full re-pricing of the position?
a. $18,280
b. $25,950
c. $29,135
d. $33,640
820.2. Springshield is a market maker who has written a straddle for a client; this is a "top straddle" or "straddle write" which entails selling a call and a put with the same exercise price and expiration date. While the stock price is $90.00, the options' strike price is also $90.00 and the maturity is 20 days. The stock's volatility is 18.0% and the riskless rate is 4.0%. The straddle write includes 100 option contracts, and each contract is on 100 options. The position is almost delta neutral; aka, the position delta is effectively zero. When the option maturity is twenty days, the market maker's initial position theta is 228,678 and its position gamma is -1,735. If nothing else changes (i.e., ceteris paribus such that the stock price, volatility, and riskfree rate are unchanged), what happens to market maker's position theta and gamma after ten days later, when the option maturity is only ten days?
a. Both position theta and position gamma increase
b. Position theta increases and position gamma decreases
c. Position theta decreases and position gamma increases
d. Both position theta and position gamma decrease
820.3. Consider a portfolio that is delta neutral, with a gamma of -200 and a vega (measuring sensitivity to implied volatility) of -5,000. The options shown in the following table can be traded. The portfolio can be made vega neutral by including a long position in 125 of Option 2. This would alter position delta to -48.75 and require that about 49 units of the asset be purchased to maintain delta neutrality. The gamma of the portfolio would change from -200.0 to -168.75.

Which trade(s) will neutralize delta, gamma and vega? (this is a variation on Hull's example 19.5)
a. Short 1,333 of Option 1; Short 4,750 of Option 2; plus Long 800 of the underlying asset
b: Short 900 of Option 1; Long 2,000 of Option 2; plus Long 390 of the underlying asset
F: Long 1,650 of Option 1; Long 700 of Option 2; plus Short 500 of the underlying asset
d. Long 3,000 of Option 1; Short 1,000 of Option 2; plus Short 2,100 of the underlying asset
Answers here:
Last edited by a moderator:
