Fran
Administrator
AIMs: Define, interpret, and apply a bond’s yield-to-maturity (YTM) to bond pricing. Compute a bond's YTM given a bond structure and price. Explain the relationship between spot rates and YTM. Calculate the price of an annuity and a perpetuity.
Questions:
316.1. Assume the following 2-year spot rate curve and corresponding discount function (set of discount factors):
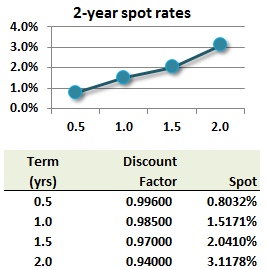
Which is nearest to the semiannually compounded yield to maturity (YTM) of a $100 par bond with two year maturity that pays a 4.0% semi-annual coupon ?
a. 2.65%
b. 2.94%
c. 3.07%
d. 3.11%
316.2. Assume the upward-sloping 2-year theoretical spot rate curve, and associated discount factors, below:
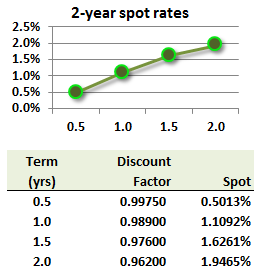
Consider three bonds with identical par value of $100 and maturity of two years:
a. YTM (I) < II < YTM (III)
b. I = II = III (same YTM)
c. III < II < I
d. Unclear without more information
316.3. Sarah won a lottery that gives her a choice between two payouts. Neglecting any liquidity or counterparty risk, she simply wants to select the option with the higher present value. Her choices are between an annuity and a perpetuity:
I. The annuity will pay her $1,000 every six months, six months from today, over the next ten years; i.e., equivalent to a 2.0% semiannual coupon on $100,000 notional.
II. A perpetuity will pay her $500 every six months but forever
The yield curve happens to be conveniently flat at 8.0% at all maturities. The annuity does not pay anything beyond the final $1,000 "coupon" which is why we might refer to a "notional" rather than a "principal." Which of the following is correct?
a. The annuity has a higher present value regardless of the yield
b. The annuity has a higher present value at the current 8.0% yield but not necessarily at any yield
c. The perpetuity has a higher present value regardless of the yield
d. The perpetuity has a higher present value at the current 8.0% yield but not necessarily at any yield
Answers:
Questions:
316.1. Assume the following 2-year spot rate curve and corresponding discount function (set of discount factors):

Which is nearest to the semiannually compounded yield to maturity (YTM) of a $100 par bond with two year maturity that pays a 4.0% semi-annual coupon ?
a. 2.65%
b. 2.94%
c. 3.07%
d. 3.11%
316.2. Assume the upward-sloping 2-year theoretical spot rate curve, and associated discount factors, below:

Consider three bonds with identical par value of $100 and maturity of two years:
- Bond I is a zero-coupon bond
- Bond II pays a semi-annual 2.0% coupon
- Bond III pays a semi-annual 4.0% coupon
a. YTM (I) < II < YTM (III)
b. I = II = III (same YTM)
c. III < II < I
d. Unclear without more information
316.3. Sarah won a lottery that gives her a choice between two payouts. Neglecting any liquidity or counterparty risk, she simply wants to select the option with the higher present value. Her choices are between an annuity and a perpetuity:
I. The annuity will pay her $1,000 every six months, six months from today, over the next ten years; i.e., equivalent to a 2.0% semiannual coupon on $100,000 notional.
II. A perpetuity will pay her $500 every six months but forever
The yield curve happens to be conveniently flat at 8.0% at all maturities. The annuity does not pay anything beyond the final $1,000 "coupon" which is why we might refer to a "notional" rather than a "principal." Which of the following is correct?
a. The annuity has a higher present value regardless of the yield
b. The annuity has a higher present value at the current 8.0% yield but not necessarily at any yield
c. The perpetuity has a higher present value regardless of the yield
d. The perpetuity has a higher present value at the current 8.0% yield but not necessarily at any yield
Answers:

