Learning Objectives: Describe the principal components analysis and explain its use in understanding term structure movements. Calculate the KR01s of a portfolio given a set of key rates. Apply key rate analysis and principal components analysis to estimating portfolio volatility.
Questions:
24.16.1. An investment bank's risk analyst uses principal components analysis (PCA) to assess swap rates and create a hedged butterfly trade. Based on the analysis, the analyst recommends a strategy where the bank acts as a payer in a 5-year swap and a receiver in both 2-year and 10-year swap contracts to capitalize on a perceived mispricing of the 5-year swap rate.
The PCA results for a 1 standard deviation increase in each component show the following changes in basis points for different maturities:
a. Increase the notional amount of the 2-year swap to hedge against the level component and decrease the 10-year swap to adjust for the slope component.
b. Assign equal notional amounts to the 2-year and 10-year swaps to uniformly distribute exposure across the term structure.
c. Opt for a higher notional amount in the 10-year swap compared to the 2-year swap to better counterbalance the level component's stronger impact on longer maturities.
d. Use the PCA results to calculate specific notional amounts that exactly neutralize the bank's exposure to both the level and slope components, as described in a detailed hedge strategy.
24.16.2. A risk manager at a bank is measuring the sensitivity of a bond portfolio to nonparallel shifts in spot rates. The portfolio currently holds a 4-year zero coupon bond and a 7-year zero coupon bond with the following sensitivities to these respective spot rates:
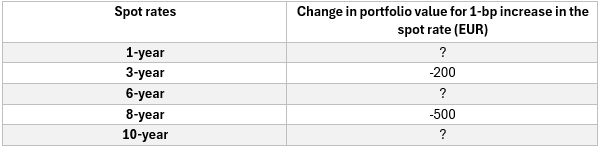
To approximate the non-parallel movement of the spot rate curve, the manager treats the 1-year, 6-year, and 10-year spot rates as key rates.
Given this information, what is the portfolio’s key rate 01 (KR01) for a 1-bp increase in the 6-year rate?
a. -EUR370
b. -EUR380
c. -EUR330
d. -EUR500
24.16.3. A risk analyst at a financial institution is tasked with estimating portfolio volatility by applying principal components analysis (PCA) and key rate analysis. The PCA has identified three significant factors—level, slope, and curvature—that explain 97.6% of the variance in Treasury rate movements. The analyst has also determined the sensitivity of the portfolio to hypothetical movements in these factors, quantified as changes in portfolio value:
a. $82,447
b. $170,259
c. $427.39
d. $182,666
Answers here:
Questions:
24.16.1. An investment bank's risk analyst uses principal components analysis (PCA) to assess swap rates and create a hedged butterfly trade. Based on the analysis, the analyst recommends a strategy where the bank acts as a payer in a 5-year swap and a receiver in both 2-year and 10-year swap contracts to capitalize on a perceived mispricing of the 5-year swap rate.
The PCA results for a 1 standard deviation increase in each component show the following changes in basis points for different maturities:
- Level Component - Increases all rates, having the greatest impact on mid to long-term rates.
- Slope Component - Decreases short-term rates more than long-term rates, steepening the term structure.
- Short Rate Component - Primarily affects short-term rates with minimal impact on long-term rates.
a. Increase the notional amount of the 2-year swap to hedge against the level component and decrease the 10-year swap to adjust for the slope component.
b. Assign equal notional amounts to the 2-year and 10-year swaps to uniformly distribute exposure across the term structure.
c. Opt for a higher notional amount in the 10-year swap compared to the 2-year swap to better counterbalance the level component's stronger impact on longer maturities.
d. Use the PCA results to calculate specific notional amounts that exactly neutralize the bank's exposure to both the level and slope components, as described in a detailed hedge strategy.
24.16.2. A risk manager at a bank is measuring the sensitivity of a bond portfolio to nonparallel shifts in spot rates. The portfolio currently holds a 4-year zero coupon bond and a 7-year zero coupon bond with the following sensitivities to these respective spot rates:

To approximate the non-parallel movement of the spot rate curve, the manager treats the 1-year, 6-year, and 10-year spot rates as key rates.
Given this information, what is the portfolio’s key rate 01 (KR01) for a 1-bp increase in the 6-year rate?
a. -EUR370
b. -EUR380
c. -EUR330
d. -EUR500
24.16.3. A risk analyst at a financial institution is tasked with estimating portfolio volatility by applying principal components analysis (PCA) and key rate analysis. The PCA has identified three significant factors—level, slope, and curvature—that explain 97.6% of the variance in Treasury rate movements. The analyst has also determined the sensitivity of the portfolio to hypothetical movements in these factors, quantified as changes in portfolio value:
- Level Factor: +$20,000 change for a 1-standard deviation movement.
- Slope Factor: +$35,000 change for a 1-standard deviation movement.
- Curvature Factor: -$10,000 change for a 1-standard deviation movement.
- Level Factor: 2.1358
- Slope Factor: 4.662
- Curvature Factor: 2.322
a. $82,447
b. $170,259
c. $427.39
d. $182,666
Answers here:
