Learning Objectives: Describe a one-factor interest rate model and identify common examples of interest rate factors. Calculate the DV01, duration, and convexity of a portfolio of fixed-income securities. Describe an example of hedging based on effective duration and convexity.
Questions:
24.13.1. According to the one-factor interest rate model described in the GARP material, how do changes in a single interest rate affect the term structure of interest rates?
a. All interest rates change by a different amount depending on their maturity; thus, the term structure always remains upward-sloping.
b. Changes in one interest rate lead to uniform changes across all maturities, keeping the shape of the term structure constant.
c. A change in a single rate results in non-parallel shifts where short-maturity rates change more significantly than long-maturity rates, potentially altering the slope of the term structure.
d. Interest rate changes do not affect the term structure as each maturity responds independently to market forces.
24.13.2. An analyst at Axiom Bond Fund is calculating the sensitivity of a 3-year 4% US treasury bond to changes in interest rates. His supervisor suggests he find DV01. The nominal value of bond holding is 1,000,000.
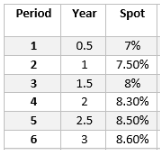
What should be the DV01?
a. 480.68
b. 240.34
c. 392.00
d. 784.00
24.13.3. Sam Bank has calculated the DV01 of its position to be -USD 463. To hedge its position, the bank considers adding a 10% coupon bond with a face value of USD 1 million, which has a DV01 of USD 265.72. The bank aims to perfectly hedge its position against small parallel shifts in the term structure of interest rates.
Based on the information provided, calculate the size of the position in the 10% coupon bond the bank should establish to exactly hedge its DV01 exposure.
a. USD 1,742,436
b. USD 573,909
c. USD 1,000,000
d. USD 0
Answers here:
Questions:
24.13.1. According to the one-factor interest rate model described in the GARP material, how do changes in a single interest rate affect the term structure of interest rates?
a. All interest rates change by a different amount depending on their maturity; thus, the term structure always remains upward-sloping.
b. Changes in one interest rate lead to uniform changes across all maturities, keeping the shape of the term structure constant.
c. A change in a single rate results in non-parallel shifts where short-maturity rates change more significantly than long-maturity rates, potentially altering the slope of the term structure.
d. Interest rate changes do not affect the term structure as each maturity responds independently to market forces.
24.13.2. An analyst at Axiom Bond Fund is calculating the sensitivity of a 3-year 4% US treasury bond to changes in interest rates. His supervisor suggests he find DV01. The nominal value of bond holding is 1,000,000.

What should be the DV01?
a. 480.68
b. 240.34
c. 392.00
d. 784.00
24.13.3. Sam Bank has calculated the DV01 of its position to be -USD 463. To hedge its position, the bank considers adding a 10% coupon bond with a face value of USD 1 million, which has a DV01 of USD 265.72. The bank aims to perfectly hedge its position against small parallel shifts in the term structure of interest rates.
Based on the information provided, calculate the size of the position in the 10% coupon bond the bank should establish to exactly hedge its DV01 exposure.
a. USD 1,742,436
b. USD 573,909
c. USD 1,000,000
d. USD 0
Answers here:
